Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m (H.9.27).
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
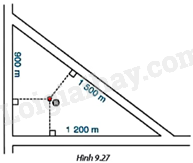
a) + Chu vi phần đất giới hạn bởi tam giác trên là tổng của ba cạnh tam giác.
+ Chứng minh phần đất giới hạn bởi tam giác là tam giác vuông.
+ Khi đó, diện tích phần đất giới hạn bởi tam giác đó bằng nửa tích hai cạnh góc vuông.
b) Gọi tam giác giới hạn phần đất là ABC, trong đó \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
+ Khách sạn nằm ở vị trí tâm đường tròn nội tiếp tam giác ABC.
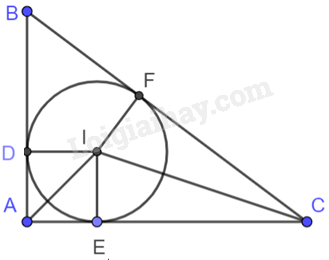
+ Từ I kẻ ID vuông góc với AB tại D, IE vuông góc với AC tại E, IF vuông góc với BC.
+ Chứng minh tứ giác AEID là hình vuông.
+ Đặt ID = IE = AE = DA = r.
+ Sử dụng tính chất của hai tiếp tuyến cắt nhau để tìm r
a) Vì \({900^2} + 1\;{200^2} = 1\;{500^2}\) nên tam giác này là tam giác vuông.
Diện tích phần đất giới hạn bởi tam giác trên là:
\(S = \frac{1}{2}.900.1\;200 = 540\;000\left( {{m^2}} \right)\)
Chu vi phần đất giới hạn bởi tam giác trên là:
\(900 + 1\;200 + 1\;500 = 3\;600\left( m \right)\)
b) Để khách sạn cách đều cả ba con đường thì khách sạn đó trùng với tâm đường tròn nội tiếp tam giác giới hạn phần đất.
Gọi tam giác giới hạn phần đất là ABC, trong đó, \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
Do đó, tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giác ABC.
Từ I kẻ ID vuông góc với AB tại D, IE vuông góc với AC tại E, IF vuông góc với BC tại F.
Khi đó, \(ID = IE = IF\).
Vì ID vuông góc với AB tại D, IE vuông góc với AC tại E nên \(\widehat {IEA} = \widehat {IDA} = {90^o}\).
Tứ giác ADIE có: \(\widehat {EAD} = \widehat {IEA} = \widehat {IDA} = {90^o}\) nên tứ giác ADIE là hình chữ nhật. Mà \(ID = IE\) nên tứ giác ADIE là hình vuông.
Do đó, \(ID = IE = AE = AD = r\)
Ta có: \(EC = AC - AE = 1200 - AE = 1200 - r\), \(BD = AB - AD = 900 - r\)
Vì CE và CF là hai tiếp tuyến cắt nhau của (O) nên CE = CF.
Vì BF và BA là hai tiếp tuyến cắt nhau của (O) nên BD = BF.
Mà BF + CF = BC = 1500 nên ta có:
\(900 - r + 1200 - r = 1500\)
\(2100 - 2r = 1500\)
\(2r = 600\)
\(r = 300\)
Do đó, khách sạn cách mỗi con đường 300m.
Các bài tập cùng chuyên đề
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat {EIF} + \widehat {BAC} = {180^o}\)
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {BOC} = {120^o}\) và \(\widehat {OCA} = {20^o}\). Tính số đo các góc của tam giác ABC.
Cho ABC là tam giác đều có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
Cho hình vuông ABCD có cạnh bằng 4cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.
Cho tam giác đều ABC có cạnh bằng 6 cm.
a) Nêu các vẽ đường tròn ngoại tiếp tam giác ABC.
b) Nêu các vẽ đường tròn nội tiếp tam giác ABC.
c) Tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).
a) Chứng minh OI vuông góc với BC.
b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).
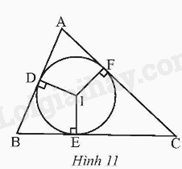
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).
a) Chứng minh 2AD = AB + AC – BC.
b) Tìm các hệ thức tương tự như ở câu a.
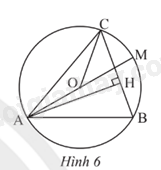
Cho tam giác nhọn ABC có đường cao AH (H \( \in \) BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh \(\widehat {OAC} = \widehat {BAH}\).
Trong các hình 15a, 15b, 15c, 15d ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?
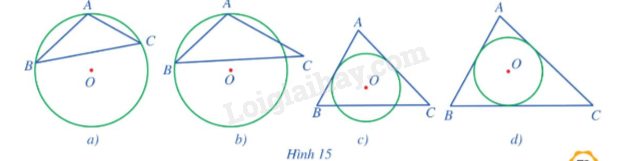
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh:
a) Ba điểm I, H, K thẳng hàng.
b) AM = AN.
c) \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)
Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh:
a)\(\widehat {CBM} = \widehat {CAK}\)
b) Tam giác BHN cân.
c) BC là đường trung trực của HN.
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn \(\widehat {BAC} = 30^\circ \) (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?
Tam giác đều ABC có cạnh bằng 6 cm. Tính tổng chu vi của \(\Delta \)ABC, chu vi đường tròn nội tiếp và chu vi đường tròn ngoại tiếp của nó. Từ đó trả lời câu hỏi của bài toán ở phần Khởi động.
Phần Khởi động: Bạn Uyên dùng một sợi thép để uốn thành mẫu hoạ tiết (Hình 7.1). Độ dài của sợi thép ít nhất là bao nhiêu để tam giác đều trong mẫu hoạ tiết có cạnh bằng 6 cm?
Tính bán kính của đường tròn nội tiếp, đường tròn ngoại tiếp tam giác đều có cạnh là:
a) 3 cm;
b) \(\sqrt 6 \)cm
Chứng minh rằng nếu tam giác có tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp trùng nhau thì tam giác đó là tam giác đều.
Tính chu vi của đường tròn nội tiếp và đường tròn ngoại tiếp tam giác đều ABC có cạnh bằng \(3\sqrt 2 \) cm. Diện tích của các hình tròn là bao nhiêu?
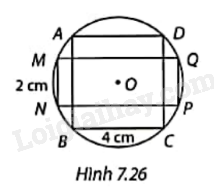
Hình vuông ABCD có cạnh 4 cm và hình chữ nhật MNPQ có chiều rộng 2 cm cùng nội tiếp trong đường tròn (O) (Hình 7.26). Tính chiều dài MQ của hình chữ nhật.
Cho tam giác $ABC$ đều cạnh bằng $6\,cm$, ba đường trung tuyến $AM,\,BN,\,CP$ cắt nhau tại $O$.
