Công thức \(E = \frac{1}{2}m{v^2}\left( J \right)\) được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Giả sử một quả bóng có khối lượng 2kg đang bay với vận tốc 6m/s. Tính động năng của quả bóng đó.
b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5kg là 48J, hãy tính vận tốc bay của quả bóng đó.
a) Thay \(m = 2,v = 6\) vào công thức \(E = \frac{1}{2}m{v^2}\), ta tìm được E.
b) Thay \(m = 1,5kg,E = 48\) vào công thức \(E = \frac{1}{2}m{v^2}\), ta tìm được v.
a) Thay \(m = 2,v = 6\) vào công thức \(E = \frac{1}{2}m{v^2}\) ta có: \(E = \frac{1}{2}{.2.6^2} = 36\left( J \right)\)
Vậy động năng của quả bóng là 36J.
b) Thay \(m = 1,5kg,E = 48\) vào công thức \(E = \frac{1}{2}m{v^2}\) ta có: \(48 = \frac{1}{2}.1,5.{v^2}\), suy ra \({v^2} = 64\), do đó \(v = 8\) (do \(v > 0\))
Vậy vận tốc bay của quả bóng là 8m/s khi động năng của quả bóng đang bay có khối lượng 1,5kg là 48J.
Chú ý khi giải: Vận tốc của vật trong chuyển động không âm, tức là \(v > 0\).
Các bài tập cùng chuyên đề
Khi thả một vật rơi tự do và bỏ qua sức cản của không khí, quãng đường của chuyển động s (mét) của vật được cho bằng công thức \(s = 4,9{t^2}\), trong đó t là thời gian chuyển động của vật (giây).
a) Hoàn thành bảng sau vào vở:
b) Giả sử một vật rơi tự do từ độ cao 19,6m so với mặt đất. Hỏi sau bao lâu vật chạm đất?
a) Viết công thức tính diện tích S của hình tròn bán kính r.
b) Hoàn thành bảng sau vào vở (lấy \(\pi = 3,14\) và làm tròn kết quả đến chữ số thập phân thứ hai):
Cho hàm số \(y = - \frac{3}{2}{x^2}\). Hoàn thành bảng giá trị sau vào vở:
Cho hàm số \(y = 0,25{x^2}\). Hoàn thành bảng giá trị sau vào vở:
Cho hàm số \(y = \frac{1}{2}{x^2}\). Hoàn thành bảng giá trị sau:
Lập bảng giá trị của hai hàm số \(y = \frac{1}{4}{x^2}\)và \(y = - \frac{1}{4}{x^2}\) với x lần lượt bằng – 4; -2; 0; 2; 4.
Cho hàm số \(y = a{x^2}\).
a) Tìm a khi biết x = 2 thì y = - 1.
b) Tính các giá trị tương ứng của hàm số trong bảng 6.1
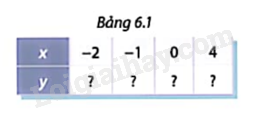
a) Cho hàm số \(y = \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.2
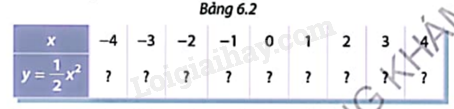
Đánh dấu các điểm (x;y) trong Bảng 6.2 trên mặt phẳng toạ độ.
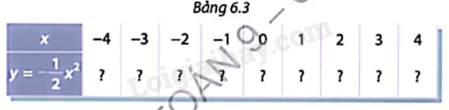
b) Cho hàm số \(y = - \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.3
Cầu treo Sunshine Skyway bắc qua Vịnh Tampa ở bang Florida (Mỹ) được hỗ trợ bởi 21 dây cáp làm bằng thép, mỗi dây có đường kính 9inch. Khối lượng mà mỗi dây cáp có thể chịu được là \(w = 8{d^2}\) (tấn), trong đó d là đường kính của dây cáp (tính bằng inch) (Theo Algebra 2, NXB McGraw-Hill, 2018).
a) Tính khối lượng tối đa mà cây cầu treo có thể chịu đựng được.
b) Nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì đường kính của dây cáp phải là bao nhiêu?
Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là \(F = a{v^2}\) (a là hằng số). Biết rằng khi tốc độ gió bằng 2m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 120N.
a) Tính hằng số a.
b) Hỏi khi tốc độ gió \(v = 15m/s\) thì lực thổi F của gió bằng bao nhiêu?
c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 12 000N, hỏi chiếc thuyền đó có thể đi được trong gió bão với tốc độ gió 90km/h không?
Xác định hệ số a của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), biết đồ thị của hàm số đi qua điểm:
a) \(A\left( { - \frac{1}{2}; - \frac{3}{2}} \right)\);
b) \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{4}} \right)\).
Nhiệt lượng toả ra trong dây dẫn được tính bởi công thức: Q = 0,24I2Rt, trong đó Q là nhiệt lượng tính bằng calo (cal), R là điện trở tính bằng ôm \(\left( \Omega \right)\), I là cường độ dòng điện tính bằng ampe (A), t là thời gian tính bằng giây.
Xét dòng điện chạy qau một dây dẫn có điện trở R = 10 \(\Omega \) trong thời gian 1 giây.
a) Hoàn thành bảng giá trị sau:
b) Tính cường độ dòng điện trong dây dẫn khi nhiệt lượng toả ra là 135 calo.
Cho hàm số y = x2. Khi y = 4 thì
A. x = - 2
B. x = - 2 hoặc x = 2
C. x = - 4 hoặc x = 4
D. x = 2
Đồ thị hàm số y = ax2 (\(a \ne 0)\) đi qua điểm A(1; - 2). Giá trị của a bằng
A. 2
B. - 2
C. \(\frac{1}{4}\)
D. \( - \frac{1}{4}\)
Cho hàm số \(y = 0,25{x^2}\). Hoàn thành bảng giá trị sau vào vở:
Diện tích toàn phần \(S\left( {c{m^2}} \right)\) của hình lập phương, tức là tổng diện tích xung quanh và diện tích đáy hai mặt của hai mặt đáy là một hàm số của độ dài cạnh a (cm).
a) Viết công thức của hàm số này.
b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là \(54c{m^2}\).
Khi bỏ qua sức cản của không khí, một vật rơi tự do sau t giây thì rơi được quãng đường \(s = 4,9{t^2}\;\left( m \right)\). Bạn Minh thả một hòn đá rơi từ miệng giếng xuống một cái giếng cạn sâu 100m.
a) Hỏi sau 1 giây, 2 giây, 3 giây, 4 giây thì hòn đá lần lượt cách đáy giếng bao nhiêu mét?
b) Thời gian từ lúc hòn đá bắt đầu rơi đến lúc chạm đáy giếng là bao lâu (làm tròn đến hàng phần mười của giây)?
Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là \(F = a{v^2}\) (a là hằng số). Biết rằng khi tốc độ gió bằng 3m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 270N.
a) Tính hằng số a.
b) Hỏi khi tốc độ gió \(v = 10m/s\) thì lực thổi F của gió bằng bao nhiêu?
c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 10 000N, hỏi chiếc thuyền đó có thể đi được trong gió bão với tốc độ gió 72km/h không?
Công thức \(E = \frac{1}{2}m{v^2}\left( J \right)\) được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Giả sử một quả bóng có khối lượng 2kg đang bay với vận tốc 6m/s. Tính động năng của quả bóng đó.
b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5kg là 48J, hãy tính vận tốc bay của quả bóng đó.
Diện tích toàn phần của hình lập phương cạnh a được cho bởi công thức \(S = 6{a^2}\).
a) Tính các giá trị của S rồi hoàn thiện bảng sau:
b) Tính cạnh a của hình lập phương (theo đơn vị centimét và làm tròn kết quả đến hàng phần trăm), biết diện tích toàn phần của hình lập phương đó bằng 42 cm2.
Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian. Liên hệ giữa quãng đường chuyển động s (mét) và thời gian chuyển động x (giây) được cho bởi hàm số \(s = 4,9{x^2}\). Người ta thả một vật nặng từ độ cao 56 m trên tháp nghiêng Pi-sa xuống đất (sức cản của không khí không đáng kể).
a) Hỏi sau thời gian 2,5 giây vật nặng còn cách mặt đất bao nhiêu mét?
b) Khi vật nặng còn cách mặt đất 17,584 m thì nó đã rơi thời gian bao nhiêu giây?
Một viên bi lăn trên mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian
bởi hàm số \(y = a{t^2}\) (t tính bằng giây, y tính bằng mét). Người ta đo được quãng đường viên bi lăn được ở thời điểm 3 giây là 2,25 m. Hỏi khi viên bi lăn được quãng đường 6,25 m thì nó đã lăn trong bao lâu?
a) Điểm \(A\left( {0,2;1} \right)\) thuộc đồ thị hàm số nào trong các hàm số sau:
\(y = 10{x^2};y = - 10{x^2};\) \(y = 25{x^2};\) \(y = - 25{x^2};\) \(y = \frac{1}{{25}}{x^2};\) \(y = - \frac{1}{{25}}{x^2}\)
b) Trong các điểm \(B\left( { - 2;4\sqrt 3 } \right);\) \(C\left( { - 2; - 4\sqrt 3 } \right);\) \(D\left( { - 0,2; - 0,4\sqrt 3 } \right);\) \(E\left( {0,4\sqrt 3 ;0,2} \right)\), điểm nào thuộc đồ thị hàm số \(y = - \sqrt 3 {x^2}\).
Cho A là giao điểm của hai đường thẳng \(y = x - 1\) và \(y = - 2x + 8\). Chứng minh rằng điểm A thuộc đồ thị hàm số \(y = \frac{2}{9}{x^2}\).
