Một mảnh vườn hình chữ nhật có chiều rộng nhỏ hơn chiều dài 6m và có diện tích là \(280{m^2}\). Tính các kích thước của mảnh vườn đó.

Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(y = x + 3 - m\) cắt parabol \(y = {x^2}\) tại hai điểm phân biệt.

Giải các phương trình sau:

a) \(2{x^2} + \frac{1}{3}x = 0\);

b) \({\left( {3x + 2} \right)^2} = 5\).

Không cần giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức \(\Delta \) và xác định số nghiệm của mỗi phương trình sau:

a) \(11{x^2} + 13x - 1 = 0\);

b) \(9{x^2} + 42x + 49 = 0\);

c) \({x^2} - 2x + 3 = 0\).

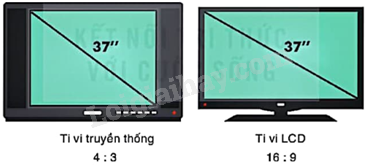
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.

Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:

a) \({x^2} - 2\sqrt 5 x + 1 = 0\);

b) \(3{x^2} - 9x + 3 = 0\);

c) \(11{x^2} - 13x + 5 = 0\);

d) \(2{x^2} + 2\sqrt 6 x + 3 = 0\).

a) Bằng cách đưa về dạng phương trình tích, hãy giải các phương trình sau:

i) \(3{x^2} - 12x = 0\)

ii) \({x^2} - 16 = 0\)

b) Để đưa các phương trình bậc hai dạng đặc biệt trên về phương trình tích ta đã dùng phép biến đổi nào?

Giải các phương trình:

a) \(3{x^2} - 27 = 0\)

b) \({x^2} - 10x + 25 = 16\)

Giải các phương trình:

a) \(5{x^2} + 7x = 0\)

b) \(5{x^2} - 15 = 0\)

Dùng công thức nghiệm để giải các phương trình sau và kiểm tra kết quả bằng máy tính cầm tay.

a) \({x^2} - x - 20 = 0\)

b) \(6{x^2} - 11x - 35 = 0\)

c) \(16{y^2} + 24y + 9 = 0\)

d) \(3{x^2} + 5x + 3 = 0\)

e) \({x^2} - 2\sqrt 3 x - 6 = 0\)

g) \({x^2} - \left( {2 + \sqrt 3 } \right)x + 2\sqrt 3  = 0\)

Giải các phương trình

a) \({x^2} - x - 5 = 0\)

b) \(2{x^2} - 0,5x - 0,03 = 0\)

c) \( - 16{x^2} + 8x - 1 = 0\)

d) \( - 2{x^2} + 5x - 4 = 0\)

e) \(\frac{1}{5}{x^2} - 5 = 0\)

g) \(3{x^2} + \sqrt 2 x = 0\)

Mảnh đất của bác An có dạng hình chữ nhật với chiều dài hơn chiều rộng 10m. Ở mỗi góc của mảnh đất, bác An đã dành 1 phần đất có dạng tam giác vuông cân với cạnh góc vuông bằng \(\frac{1}{8}\) chiều rộng của mảnh đất để trồng hoa (Hình 8). Tính chiều rộng mảnh đất đó, biết diện tích còn lại của mảnh đất không tính phần trồng hoa là 408 \({m^2}.\)

Phân tích vế trái của các phương trình sau thành nhân tử rồi giải các phương trình đó:

a) 2x – x² = 0;

b) \({x^2} - 6x + 9 = \frac{1}{2}\)

Giải các phương trình sau:

a) 3x² = - 4x;

b) \(2{x^2} - 3 = 0\)

Giải các phương trình sau:

a) \(2{x^2} + 3x - 7 = x(x + 3)\)

b) \(\frac{{x(x - 1)}}{3} + 2 = \frac{{x + 5}}{4}\).

Phương trình nào sau đây có nghiệm x = 2?

A. \({x^2} - 6x + 5 = 0\)

B. \({x^2} - 5x + 6 = 0\)

C. \(2{x^2} + 3x - 2 = 0\)

D. \(3{x^2} + 5x + 2 = 0\)

Không cần giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức \(\Delta \) và xác định số nghiệm của mỗi phương trình sau:

a) \(11{x^2} + 13x - 1 = 0\);

b) \(9{x^2} + 42x + 49 = 0\);

c) \({x^2} - 2x + 3 = 0\).

Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:

a) \({x^2} - 2\sqrt 5 x + 1 = 0\);

b) \(3{x^2} - 9x + 3 = 0\);

c) \(11{x^2} - 13x + 5 = 0\);

d) \(2{x^2} + 2\sqrt 6 x + 3 = 0\).

Giải các phương trình:

a) \(2{x^2} - 7x = 0;\)

b) \(- {x^2} + \sqrt 8 x - \sqrt {21}  = 0;\)

c) \(- \sqrt 5 {x^2} + 2x + 3\sqrt 5  = 0;\)

d) \(1,5{x^2} - 0,4x - 1,2 =  - 1,1{x^2} + 1;\)

e) \(\left( {\sqrt 7  - 2} \right){x^2} + 3x + 10 = {x^2} + 10;\)

g) \(- \sqrt {32} {x^2} - 4x + \sqrt 2  = \sqrt 2 {x^2} + x - \sqrt 8 \)