Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
-
A.
\(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
-
B.
\(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
-
C.
\(\cos \alpha = \frac{{ \pm \sqrt 3 }}{2}\).
-
D.
Cả A, B, C đều sai.
Sử dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Sử dụng đường tròn lượng giác để xét dấu $\cos \alpha$.
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = \pm \sqrt {1 - {{\sin }^2}\alpha } = \pm \frac{{\sqrt 3 }}{2}\).
Mà \(\frac{\pi }{2} < \alpha < \pi \) nên điểm cuối của \(\alpha\) thuộc góc phần tư thứ II, suy ra \(\cos \alpha < 0\). Do đó, \(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
Đáp án : A
Dấu của các giá trị lượng giác của \(\alpha = (OA,OM)\), phụ thuộc vào vị trí điểm M trên đường tròn lượng giác:
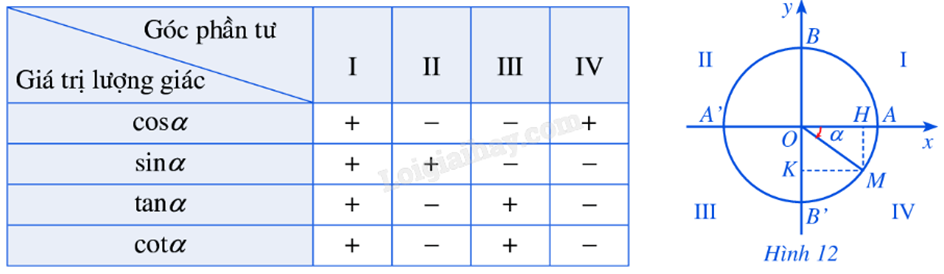

Các bài tập cùng chuyên đề
Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp trương (tức là áp lực máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức:
\(B(t) = 80 + 7.\sin \frac{{\pi t}}{{12}}\)
Trong đó t là số giờ tính từ lúc nửa đêm và B(t) tính bằng mmHg (milimét thủy ngân). Tìm huyết áp tâm trương của người này vào cá thời điểm sau:
a) 6 giờ sáng;
b) 10 giờ 30 phút sáng;
c) 12 giờ trưa;
d) 8 giờ tối.
Tính: a) \(\sin ( - {675^ \circ })\) b) \(\tan \frac{{15\pi }}{4}\)
Xét hai điểm M, N trên đường tròn lượng giác xác định bởi hai góc đối nhau (H1.12a).
a) Có nhận xét gì về vị trí của hai điểm M, N đổi với hệ trục Oxy. Từ đó rút ra liên hệ giữa \(\cos ( - \alpha )\) và \(\cos \alpha \); \(\sin ( - \alpha )\)và \(\sin \alpha \)
b) Từ kết quả HĐ6a, rút ra liên hệ giữa: \(\tan ( - \alpha )\) và \(\tan \alpha \); \(\cot ( - \alpha )\) và \(\cot \alpha \)
Tính các giá trị lượng giác của góc \(\alpha \), biết \(\cos \alpha = - \frac{2}{3}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
a) Dựa vào định nghĩa của \(\sin \alpha \)và \(\cos \alpha \) hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \)
b) Sử dụng kết quả của HĐ5a và định nghĩa của \(\tan \alpha \), hãy tính \(1 + {\tan ^2}\alpha \)
Trong các khẳng định sau, khẳng định nào là sai?
A. \(\sin \left( {\pi - \alpha } \right) = \sin \alpha \)
B. \(\cos \left( {\pi - a} \right) = \cos \alpha \)
C. \(\sin \left( {\pi + \alpha } \right) = - \sin \alpha \).
D. \(\cos (\pi + \alpha ) = - \cos \alpha \)
Cho góc lượng giác \(\alpha \). So sánh
a) \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\) và 1
b) \(\tan \alpha .\cot \alpha \,\,\) và 1 với \(\cos \alpha \ne 0;\sin \alpha \ne 0\)
c) \(1 + {\tan ^2}\alpha \,\,\) và \(\frac{1}{{{{\cos }^2}\alpha }}\) với \(\cos \alpha \ne 0\)
d) \(1 + {\cot ^2}\alpha \,\) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với \(\sin \alpha \ne 0\)
Cho góc lượng giác \(\alpha \)sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm \(\cos \alpha \)
Tính các giá trị lượng giác của góc \(\alpha \) trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\) với \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = - \frac{2}{3}\) với \( - \pi < \alpha < 0\)
c) \(\tan \alpha = 3\) với \( - \pi < \alpha < 0\)
d) \(\cot \alpha = - 2\) với \(0 < \alpha < \pi \)
Cho \(\tan \alpha = \frac{2}{3}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Tính \(\cos \alpha \) và \(\sin \alpha \)
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
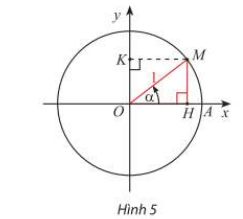
b) Chia cả hai vế của biểu thức ở câu a) cho \({\cos ^2}\alpha \) ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho \({\sin ^2}\alpha \) ta được đẳng thức nào?
Các đẳng thức sau có thể đồng thời xảy ra không?
a) \(\sin \alpha = \frac{3}{5}\) và \(\cos \alpha = - \frac{4}{5}\)
b) \(\sin \alpha = \frac{1}{3}\) và \(\cot \alpha = \frac{1}{2}\)
c) \(\tan \alpha = 3\) và \(\cot \alpha = \frac{1}{3}\)
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)
Chứng minh các đẳng thức lượng giác sau:
a) \({\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \)
b) \(\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\)
Cho \(\sin \alpha = \frac{1}{3}\) và \(0 < \alpha < \frac{\pi }{2}\). Khi đó
a) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\)
b) \(\cos \alpha = \frac{{2\sqrt 2 }}{3}\)
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\)
d) \(\cot \alpha = - 2\sqrt 2 \)
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
-
A.
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
-
B.
\(\sin \alpha = - \frac{{\sqrt {15} }}{4}\)
-
C.
\(\sin \alpha = \frac{{15}}{{16}}\)
-
D.
\(\sin \alpha = - \frac{{15}}{{16}}\)
Cho \(\sin \alpha = \frac{2}{3}\) với \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \(\cos \alpha \) là?
-
A.
\(\cos \alpha = \frac{2}{3}\)
-
B.
\(\cos \alpha = - \frac{{\sqrt 5 }}{3}\)
-
C.
\(\cos \alpha = \frac{{\sqrt 5 }}{3}\)
-
D.
\(\cos \alpha = \frac{3}{2}\)
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Đơn giản biểu thức \(A = \cos \left( {\frac{{9\pi }}{2} - \alpha } \right) + \sin \left( {\alpha - \pi } \right)\) ta được
-
A.
\(A = \cos \alpha + \sin \alpha \)
-
B.
\(A = 2\sin \alpha \)
-
C.
\(A = \sin \alpha \cos \alpha \)
-
D.
\(A = 0\)
Cho góc \(\alpha \) thỏa mãn \({\rm{tan}}\alpha + {\rm{cot}}\alpha = 2\). Giá trị của biểu thức \(P = {\rm{ta}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{t}}^2}\alpha \) là
-
A.
\(P = 1\)
-
B.
\(P = 2\)
-
C.
\(P = 3\)
-
D.
\(P = 4\)
Mệnh đề nào sau đây là sai?
-
A.
$ - 1 \leqslant \sin \alpha \leqslant 1;\,\, - 1 \leqslant \cos \alpha \leqslant 1$
-
B.
$\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\,\,(\cos \alpha \ne 0)$
-
C.
$\tan \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\,\,(\sin \alpha \ne 0)$
-
D.
${\sin ^2}\left( {2024\alpha } \right) + {\cos ^2}\left( {2024\alpha } \right) = 2024$
Cho \(\cos x = - \frac{5}{{13}}\,\,({90^o} < x < {180^o})\). Tính các giá trị lượng giác còn lại.
Cho \(\sin a + \cos a = m\). Hãy tính theo m.
a) \(\sin a\cos a\)
b) \({\sin ^3}a + {\cos ^3}a\)
c) \({\sin ^4}a + {\cos ^4}a\).
Chứng minh các đẳng thức sau:
a) \({\cos ^4}x - {\sin ^4}x = 2{\cos ^2}x - 1\);
b) \({\tan ^2}x - {\sin ^2}x = {\tan ^2}x.{\sin ^2}x\);
c) \({(\sin x + \cos x)^2} + {(\sin x - \cos x)^2} = 2\).
Rút gọn biểu thức \(A = 2{\cos ^4}x - {\sin ^4}x + {\sin ^2}x{\cos ^2}x + 3{\sin ^2}x\).
Với giá trị nào của x, mỗi đẳng thức sau đúng?
a) \(\tan x\cot x = 1\);
b) \(1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\);
c) \(1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\);
d) \(\tan x + \cot x = \frac{2}{{\sin 2x}}\).
Trong các đẳng thức sau, đẳng thức nào sai?
A. \(\sin \left( {\frac{\pi }{2} - x} \right) = \cos x\).
B. \(\sin \left( {\frac{\pi }{2} + x} \right) = \cos x\).
C. \(\tan \left( {\frac{\pi }{2} - x} \right) = \cot x\).
D. \(\tan \left( {\frac{\pi }{2} + x} \right) = \cot x\).
Trong các đẳng thức sau, đẳng thức nào đúng?
A. \(\sin \left( {{{180}^0} - a} \right) = - \cos a\).
B. \(\sin \left( {{{180}^0} - a} \right) = - \sin a\).
C. \(\sin \left( {{{180}^0} - a} \right) = \sin a\).
D. \(\sin \left( {{{180}^0} - a} \right) = \cos a\).
Biết \(\sin x = \frac{1}{2}\). Giá trị của \({\cos ^2}x\) bằng
A. \({\cos ^2}x = \frac{1}{2}\).
B. \({\cos ^2}x = \frac{{\sqrt 3 }}{2}\).
C. \({\cos ^2}x = \frac{1}{4}\).
D. \({\cos ^2}x = \frac{3}{4}\).
Biết \(\cot x = \frac{1}{2}\). Giá trị của biểu thức \(\frac{{4\sin x + 5\cos x}}{{2\sin x - 3\cos x}}\) bằng
A. \(\frac{1}{{17}}\).
B. \(\frac{5}{9}\).
C. \(13\).
D. \(\frac{2}{9}\).







Danh sách bình luận