Thực hiện phép tính \(\dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{{45}}:\left( {\dfrac{1}{5} - \dfrac{2}{{15}}} \right) + 1\dfrac{2}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\) ta được kết quả là
-
A.
\(\dfrac{{27}}{7}\)
-
B.
\(\dfrac{7}{{27}}\)
-
C.
\(\dfrac{1}{7}\)
-
D.
$\dfrac{1}{4}$
Thực hiện phép tính theo thứ tự: ngoặc tròn \( \to \) ngoặc vuông
Và nhân chia trước, cộng trừ sau.
Ta có \(\dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{{45}}:\left( {\dfrac{1}{5} - \dfrac{2}{{15}}} \right) + 1\dfrac{2}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\)
\( = \dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{{45}}:\left( {\dfrac{3}{{15}} - \dfrac{2}{{15}}} \right) + \dfrac{5}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\)
\( = \dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{{45}}:\dfrac{1}{{15}} + \dfrac{5}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\)
\( = \dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{{45}}.\dfrac{{15}}{1} + \dfrac{5}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\)
\( = \dfrac{2}{9}.\left[ {\dfrac{{ - 4}}{3} + \dfrac{5}{3}} \right] - \left( {\dfrac{{ - 5}}{{27}}} \right)\)
$ = \dfrac{2}{9}.\dfrac{1}{3} - \left( {\dfrac{{ - 5}}{{27}}} \right)$
\( = \dfrac{2}{{27}} + \dfrac{5}{{27}}\)
\( = \dfrac{7}{{27}}\)
Đáp án : B

Các bài tập cùng chuyên đề
Có hai tấm ảnh kích thước 10 cm \( \times \) 15 cm được in trên giấy ảnh kích thước 21,6 cm \( \times \)27,9 cm như Hình 1.8. Nếu cắt ảnh theo đúng kích thước thì diện tích phần giấy ảnh còn lại bao nhiêu?
Tính:
a) \(\frac{{ - 6}}{{18}} + \frac{{18}}{{27}}\);
b) \(2,5 - ( - \frac{6}{9})\);
c) \(- 0,32.( - 0,875)\);
d) \(( - 5):2\frac{1}{5}\)
Tính giá trị của các biểu thức sau:
\(\begin{array}{l}a)(8 + 2\frac{1}{3} - \frac{3}{5}) - (5 + 0,4) - (3\frac{1}{3} - 2)\\b)(7 - \frac{1}{2} - \frac{3}{4}):(5 - \frac{1}{4} - \frac{5}{8})\end{array}\)
Em hãy tìm cách “nối” các số ở những chiếc lá trong Hình 1.9 bằng dấu các phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở bông hoa.

Tính một cách hợp lí.
\(0,65.78 + 2\dfrac{1}{5}.2020 + 0,35.78 - 2,2.2020.\)
Tính giá trị của các biểu thức sau:
\(\begin{array}{l}a)A = (2 - \frac{1}{2} - \frac{1}{8}):(1 - \frac{3}{2} - \frac{3}{4});\\b)B = 5 - \frac{{1 + \frac{1}{3}}}{{1 - \frac{1}{3}}}.\end{array}\)
Tính một cách hợp lí: \(1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - 1,2.5\frac{3}{4} - \frac{{16}}{7}.\frac{{ - 71}}{8}\)
Chị Trang đang có ba tháng thực tập tại Mĩ. Gần hết thời gian thực tập, chị Trang và bạn có kế hoạch tổ chức một bữa tiệc chia tay trước khi về nước. Chị ấy dự định mua 4 cái bánh pizza, mỗi cái giá 10,25 USD. Chị Trang có phiếu giảm giá 1,5 USD cho mỗi cái bánh pizza, hãy tính tổng số tiền chị ấy dùng để mua bánh.
Một kho có 45 tấn gạo. Người quản lý kho đã xuất đi \(\frac{1}{3}\) số gạo để cứu trợ đồng bào bị bão lụt, sau đó bán đi \(7\frac{2}{5}\) tấn, cuối cùng nhập thêm 8 tấn nữa. Tính số gạo còn lại trong kho.
Tính:
a)\(\frac{2}{{15}} + \left( {\frac{{ - 5}}{{24}}} \right)\)
b) \(\left( {\frac{{ - 5}}{9}} \right) - \left( { - \frac{7}{{27}}} \right);\)
c)\(\left( { - \frac{7}{{12}}} \right) + 0,75\)
d)\(\left( {\frac{{ - 5}}{9}} \right) - 1,25\)
e)\(0,34.\frac{{ - 5}}{{17}}\)
g) \(\frac{4}{9}:\left( { - \frac{8}{{15}}} \right);\)
h)\(\left( {1\frac{2}{3}} \right):\left( {2\frac{1}{2}} \right)\)
i) \(\frac{2}{5}.\left( { - 1.25} \right)\)
k) \(\left( {\frac{{ - 3}}{5}} \right).\left( {\frac{{15}}{{ - 7}}} \right).3\frac{1}{9}\)
Tính:
a)\(0,75 - \frac{5}{6} + 1\frac{1}{2};\)
b)\(\frac{3}{7} + \frac{4}{{15}} + \left( {\frac{{ - 8}}{{21}}} \right) + \left( { - 0,4} \right);\)
c)\(0,625 + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} + \left( {\frac{{ - 5}}{7}} \right) + 1\frac{2}{3}\)
d)\(\left( { - 3} \right).\left( {\frac{{ - 38}}{{21}}} \right).\left( {\frac{{ - 7}}{6}} \right).\left( { - \frac{3}{{19}}} \right);\)
e) \(\left( {\frac{{11}}{{18}}:\frac{{22}}{9}} \right).\frac{8}{5};\)
g)\(\left[ {\left( {\frac{{ - 4}}{5}} \right).\frac{5}{8}} \right]:\left( {\frac{{ - 25}}{{12}}} \right)\)
Tính:
a)\(\frac{3}{7}.\left( { - \frac{1}{9}} \right) + \frac{3}{7}.\left( { - \frac{2}{3}} \right);\)
b)\(\left( {\frac{{ - 7}}{{13}}} \right).\frac{5}{{12}} + \left( {\frac{{ - 7}}{{13}}} \right).\frac{7}{{12}} + \left( {\frac{{ - 6}}{{13}}} \right);\)
c)\(\left[ {\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right)} \right]:\frac{5}{9} + \left( {\frac{4}{7} - \frac{1}{3}} \right):\frac{5}{9}\)
d)\(\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right);\)
e) \(\frac{3}{5} + \frac{3}{{11}} - \left( {\frac{{ - 3}}{7}} \right) + \left( {\frac{{ - 2}}{{97}}} \right) - \frac{1}{{35}} - \frac{3}{4} + \left( {\frac{{ - 23}}{{44}}} \right)\)
Tìm x, biết:
a)\(x.\frac{{14}}{{27}} = \frac{{ - 7}}{9}\)
b)\(\left( {\frac{{ - 5}}{9}} \right):x = \frac{2}{3};\)
c)\(\frac{2}{5}:x = \frac{1}{{16}}:0,125\)
d)\( - \frac{5}{{12}}x = \frac{2}{3} - \frac{1}{2}\)
Vào tháng 6, giá niêm yết một chiếc ti vi 42 inch tại một siêu thị điện máy là 8 000 000 đồng. Đến tháng 9, siêu thị giảm giá 5% cho mỗi chiếc ti vi. Sang tháng 10, siêu thị lại giảm giá thêm một lần nữa, lúc này giá một chiếc ti vi 42 inch chỉ còn 6 840 000 đồng. Hỏi tháng 10, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc ti vi so với tháng 9?
Một cửa hàng sách có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 10% tổng số tiền của hoá đơn. Bạn Lan có thẻ thành viên và bạn mua 3 quyển sách, mỗi quyển đều có giá 120 000 đồng. Bạn đưa cho cô thu ngân 350 000 đồng. Hỏi bạn Lan được trả lại bao nhiêu tiền?
Trong tầng đối lưu, nhiệt độ giảm dần theo độ cao. Cứ lên cao 100 m thì nhiệt độ không khí giảm khoảng 0,6 °C (Theo: Sách giáo khoa Địa lí 6 – 2020 – Nhà xuất bản Giáo dục Việt Nam).
a) Tính nhiệt độ không khí bên ngoài một khinh khí cầu đang bay ở độ cao 2,8 km, biết rằng nhiệt độ trên mặt đất lúc đó là 28°C.
b) Nhiệt độ bên ngoài một khinh khí cầu đang bay ở độ cao \(\frac{{22}}{5}\) km bằng - 8,5 °C. Hỏi nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay lúc đó là bao nhiêu độ C?
Em hãy tìm cách “nối” các số ở những cánh hoa bằng các dấu phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở nhị hoa.
Mẹ bạn Minh gửi tiết kiệm 300 000 000 đồng vào một ngân hàng theo thể thức kì hạn 1 năm. Hết thời hạn 1 năm, mẹ bạn Minh nhận được cả vốn lẫn lãi là 321 600 000 đồng. Tính lãi suất ngân hàng theo thể thức gửi tiết kiệm này.
Bác Thu mua ba món hàng ở một siêu thị: Món hàng thứ nhất giá 125 000 đồng và được giảm giá 30%; món hàng thứ hai giá 300 000 đồng và được giảm giá 15%; món hàng thứ ba được giảm giá 40%. Tổng số tiền bác Thu phải thanh toán là 692 500 đồng. Hỏi giá tiền món hàng thứ ba lúc chưa giảm giá là bao nhiêu?
Nhân ngày 30/4, một cửa hàng thời trang giảm giá 20% cho tất cả các sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiết của cửa hàng thì được giảm giá thêm 10% trên giá đã giảm.
a) Chị Thanh là khách hàng thân thiết của cửa hàng, chị đã đến cửa hàng mua một chiếc váy có giá niêm yết là 800 000 đồng. Hỏi chị Thanh phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Minh cũng là một khách hàng thân thiết của cửa hàng, cô đã mua một chiếc túi xách và đã phải trả số tiền là 864 000 đồng. Hỏi giá ban đầu của chiếc túi xách đó là bao nhiêu?
Tính một cách hợp lí:
a)\(\frac{7}{3}.\left( { - 2,5} \right).\frac{6}{7};\)
b)\(0,8.\frac{{ - 2}}{9} - \frac{4}{5}.\frac{7}{9} - 0,2.\)
Tính một cách hợp lí:
a)\(\frac{{ - 3}}{{10}} - 0,125 + \frac{{ - 7}}{{10}} + 1,125\);
b)\(\frac{{ - 8}}{3}.\frac{2}{{11}} - \frac{8}{3}:\frac{{11}}{9}\);
Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra \(\frac{1}{3}\) số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.
Tính diện tích mặt bằng của ngôi nhà được mô tả như Hình 7 (các số đo trên hình tính theo đơn vị mét):
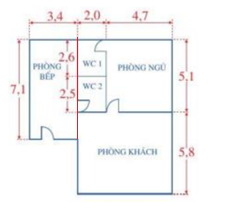
Tính một cách hợp lí:
a) \(\frac{{ - 5}}{{12}} + \left( { - 3,7} \right) - \frac{7}{{12}} - 6,3\);
b) \(2,8.\frac{{ - 6}}{{13}} - 7,2 - 2,8.\frac{7}{{13}}\)
Tìm x biết \(\frac{11}{12} - \left(\frac{2}{5} + x \right) = \frac{2}{3}\)
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{-3}{20}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(\frac{-3}{20}\)
Tính:
a) \(\dfrac{3}{{10}} + \left( {\dfrac{{ - 5}}{{12}}} \right)\)
b) \(\dfrac{{ - 3}}{8} - \left( { - \dfrac{7}{{24}}} \right)\)
c) \(\left( {\dfrac{{ - 5}}{{14}}} \right) + 0,25\)
d) \(\left( { - \dfrac{7}{8}} \right) - 1,25\)
e) \(\left( {\dfrac{{ - 5}}{{14}}} \right).\dfrac{{21}}{{25}}\)
f) \(\dfrac{8}{{27}}:\left( { - \dfrac{{16}}{{45}}} \right)\)
g) \(\left( {1\dfrac{5}{6}} \right):\left( {4\dfrac{1}{8}} \right)\)
h) \(0,38.\left( { - \dfrac{7}{{19}}} \right)\)
i) \(\left( {\dfrac{{ - 4}}{5}} \right).\left( {\dfrac{{15}}{{ - 8}}} \right).1\dfrac{1}{9}\)
Tính
a) \( - 0,375 + \dfrac{1}{4} - \left( { - \dfrac{1}{5}} \right)\)
b) \(\dfrac{2}{3} + \left( {\dfrac{{ - 5}}{{12}}} \right) + \left( {\dfrac{{ - 7}}{{15}}} \right) + ( - 0,2)\)
c) \(0,275 + \left( {\dfrac{{ - 8}}{{17}}} \right) + \dfrac{{29}}{{40}} + \left( {\dfrac{{ - 9}}{{17}}} \right) - 1\dfrac{1}{3}\)
d) \(\left( { - 5} \right).\left( {\dfrac{{ - 34}}{{21}}} \right).\left( {\dfrac{{ - 7}}{{10}}} \right).\left( { - \dfrac{3}{{17}}} \right)\)
e) \(\left( {\dfrac{{13}}{{18}}:\dfrac{{26}}{9}} \right).\dfrac{4}{7}\)
f) \(\left[ {\left( { - \dfrac{5}{{33}}} \right):\dfrac{2}{{11}}} \right].0,15\)
Tính
a) \(\dfrac{6}{7}.\left( { - \dfrac{1}{8}} \right) + \dfrac{6}{7}.\left( { - \dfrac{3}{4}} \right)\)
b) \(\left( {\dfrac{{ - 7}}{{17}}} \right).\dfrac{5}{{12}} + \left( {\dfrac{{ - 7}}{{17}}} \right).\dfrac{7}{{12}} + \left( {\dfrac{{ - 10}}{{17}}} \right)\)
c) \(\left[ {\dfrac{3}{5} + \left( {\dfrac{{ - 1}}{4}} \right)} \right]:\dfrac{3}{7} + \left[ {\left( {\dfrac{{ - 3}}{4}} \right) + \dfrac{2}{5}} \right]:\dfrac{3}{7}\)
d) \(\dfrac{7}{8}:\left( {\dfrac{2}{9} - \dfrac{1}{{18}}} \right) + \dfrac{7}{8}:\left( {\dfrac{1}{{36}} - \dfrac{5}{{12}}} \right)\)
Trong một bể nước, lượng nước chiếm đến \(\dfrac{3}{4}\)dung tích bể. Người ta mở một vòi nước chảy vào bể, mỗi giờ chảy được \(\dfrac{1}{8}\)bể. Hỏi nước chảy trong thời gian bao lâu thì đầy bể?






