Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Ôn tập chương III - Phương pháp tọa độ trong mặt phẳng
Ôn tập chương III - Phương pháp tọa độ trong mặt phẳng
Bài 4 trang 93 SGK Hình học 10
Cho đường thẳng Δ: x – y + 2 và hai điểm O(0, 0); A(2, 0)
Video hướng dẫn giải
Cho đường thẳng \(Δ: x – y + 2=0\) và hai điểm \(O(0; 0); \, A(2; 0).\)
LG a
Tìm điểm đối xứng của \(O\) qua \(Δ\)
Lời giải chi tiết:
Gọi \(H(x;y)\) là hình chiếu của \(O\) trên \(Δ\), \(\overrightarrow {OH} = (x;y)\)
\( Δ: x – y + 2 = 0\) có vecto chỉ phương \(\overrightarrow u (1;1)\)
\(\overrightarrow {OH} \bot \Delta \) \(\Rightarrow 1.x + 1.y = 0 \Leftrightarrow x + y = 0\)
Tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
x + y = 0 \hfill \cr
x - y + 2 = 0 \hfill \cr} \right. \Rightarrow H( - 1;1)\)
Gọi \(O’\) là đỉnh đối xứng của \(O\) qua \(Δ\) thì \(H\) là trung điểm của đoạn thẳng \(OO’\)
\(\eqalign{
& {x_H} = {{{x_O} + {x_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {x_{O'}}} \over 2} \cr&\Rightarrow {x_{O'}} = - 2 \cr
& {y_H} = {{{y_O} + {y_{O'}}} \over 2} \Leftrightarrow - 1 = {{0 + {y_{O'}}} \over 2}\cr& \Rightarrow {y_{O'}} = 2 \cr} \)
Vậy \(O’(-2;2)\).
Cách khác:
Gọi \(d\) là đường thẳng đi qua \(O\) và vuông góc \(\Delta \).
\(\Delta \) nhận \(\overrightarrow n = \left( {1; - 1} \right)\) làm VTPT nên nhận \(\overrightarrow u = \left( {1;1} \right)\) làm VTCP.
\(d \bot \Delta \Rightarrow \overrightarrow {{n_d}} = \overrightarrow u = \left( {1;1} \right)\) là VTPT của \(d\).
Mà \(d\) đi qua \(O\left( {0;0} \right)\) nên \(1\left( {x - 0} \right) + 1\left( {y - 0} \right) = 0\) \( \Leftrightarrow x + y = 0\)
Gọi \(H = d \cap \Delta \) thì tọa độ điểm \(H\) thỏa mãn:
\(\left\{ \begin{array}{l}x + y = 0\\x - y + 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\) \( \Rightarrow H\left( { - 1;1} \right)\)
\(O'\) đối xứng \(O\) qua \(\Delta \) hay \(H\) là trung điểm \(OO'\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_{O'}} = 2{x_H} - {x_O} = 2.\left( { - 1} \right) - 0 = - 2\\{y_{O'}} = 2{y_H} - {y_O} = 2.1 - 0 = 2\end{array} \right.\)
\( \Rightarrow O'\left( { - 2;2} \right)\).
LG b
Tìm điểm \(M\) trên \(Δ\) sao cho độ dài đường gấp khúc \(OMA\) ngắn nhất.
Lời giải chi tiết:
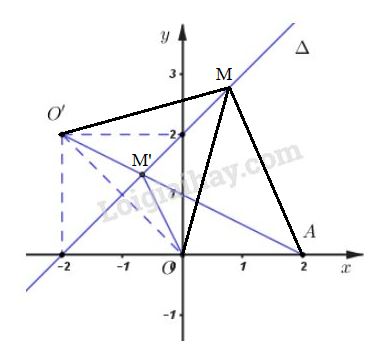
Quan sát hình vẽ ta thấy,
\(A\) và \(O\) nằm cùng phía so với \(\Delta \) hay \(A,O'\) nằm khác phía so với \(\Delta \).
Gọi \(M' = AO' \cap \Delta \) thì \(OM' = O'M'\) do \(\Delta \) là đường trung trực của \(OO'\).
Với điểm \(M\) bất kì thuộc \(\Delta \) thì \(OM + AM = O'M + AM \ge O'A\)
\( \Rightarrow {\left( {OM + MA} \right)_{\min }} = AO'\) khi \(M \equiv M'\) là giao điểm của \(AO'\) với \(\Delta \).
\(A(2; 0); O'(-2; 2)\) \( \Rightarrow \overrightarrow {AO'} = \left( { - 4;2} \right)\) là VTCP của \(AO'\) \( \Rightarrow \overrightarrow {{n_{AO'}}} = \left( {2;4} \right)\) là VTPT của \(AO'\)
Mà \(AO'\) đi qua \(A\left( {2;0} \right)\) nên \(2\left( {x - 2} \right) + 4\left( {y - 0} \right) = 0\) \( \Leftrightarrow 2x + 4y - 4 = 0\) \( \Leftrightarrow x + 2y - 2 = 0\)
\(M = AO' \cap \Delta \) \( \Leftrightarrow \left\{ \begin{array}{l}x + 2y - 2 = 0\\x - y + 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{2}{3}\\y = \dfrac{4}{3}\end{array} \right.\)
Vậy \(M\left( { - \dfrac{2}{3};\dfrac{4}{3}} \right)\)
Loigiaihay.com
- Bài 5 trang 93 SGK Hình học 10
- Bài 6 trang 93 SGK Hình học 10
- Bài 7 trang 93 SGK Hình học 10
- Bài 8 trang 93 SGK Hình học 10
- Bài 9 trang 93 SGK Hình học 10
>> Xem thêm