Câu hỏi
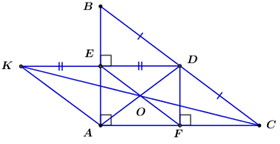
Cho \(\Delta ABC\) vuông tại \(A\) , có \(D\) là trung điểm của \(BC\) . Gọi \(E,\,F\) lần lượt là hình chiếu của \(D\) trên \(AB\) và \(AC\) .
1. Chứng minh: \(A{\rm{D}} = EF\)
2. Gọi K là điểm đối xứng với \(D\) qua \(E\) . Chứng minh ba đường thẳng \(A{\rm{D}},\,EF,\,KC\) đồng quy.
Phương pháp giải:
Áp dụng: - Dấu hiệu nhận biết hình chữ nhật
- Tính chất: hình chữ nhật, đối xứng, từ vuông góc đến song song.
Lời giải chi tiết:
1. Xét tứ giác \(A{\rm{ED}}F\) có: \(\angle BAC = \angle A{\rm{ED}} = \angle AFD = {90^0}\left( {gt} \right) \Rightarrow A{\rm{ED}}F\) là hình chữ nhật (dhnb)
\( \Rightarrow A{\rm{D}} = EF\) (tính chất hình chữ nhật)
2. Gọi \(O\) là giao điểm của \(EF\) và \(A{\rm{D}} \Rightarrow {\rm{O}}\)là trung điểm của \(EF\) và \(A{\rm{D}}\)(tính chất hình chữ nhật) (1)
\( \Rightarrow OE = OF\) (tính chất trung điểm)
Do D và K đối xứng nhau qua E nên suy ra \(\left\{ \begin{array}{l}DK \bot AB\\ED = KE\end{array} \right.\) (tính chất đối xứng)
Mà \(AC \bot AB\left( {gt} \right) \Rightarrow DK//AC\) (từ vuông góc đến song song)
Ta có: \(ED\) là đường trung bình của \(\Delta ABC\) (E, D là
trung điểm của AB, BC (gt))
\( \Rightarrow ED = \frac{1}{2}BC \Rightarrow BC = 2ED.\)
Xét tứ giác \(AKDC\) ta có:
\(\begin{array}{l}BC//KD\;\;\left( {cmt} \right)\\KD = BC\;\;\left( { = 2KD} \right)\end{array}\)
\( \Rightarrow AKDC\) là hình bình hành (dhnb)
\( \Rightarrow KC,\;EF\) cắt nhau tại trung điểm của mỗi đường (tính chất)
Mà O là trung điểm của EF (cách gọi)
\( \Rightarrow KC,\;\;EF,\;\;AD\) đồng quy tại \(O.\) (đpcm)