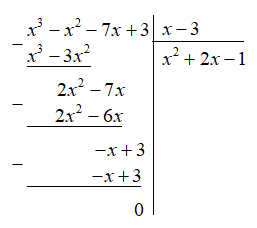Câu hỏi
a) Thực hiện phép chia đa thức \(A={{x}^{3}}-7x+3-{{x}^{2}}\) cho đa thức \(B=x-3\) .
b) Gọi Q là thương của phép chia A cho B. Chứng minh \(Q+3\) luôn nhận giá trị dương với mọi \(x\ne 3.\)
- A a) \(x^2-2x+9\)
- B a) \(x^2-2x-6\)
- C a) \(x^2-2x+1\)
- D a) \(x^2+3x+1\)
Phương pháp giải:
- Áp dụng qui tắc chia đa thức cho đa thức.
- Áp dụng tính chất: \({{A}^{2}}+k>0\) với \(\forall x\)
Lời giải chi tiết:
a) Thực hiện phép chia đa thức \(A={{x}^{3}}-7x+3-{{x}^{2}}\) cho đa thức \(B=x-3\) .
b) Ta có:
\(Q={{x}^{2}}+2\text{x}-1\Rightarrow Q+3={{x}^{2}}+2x-1+3={{x}^{2}}+2x+2\)
\(\Rightarrow Q={{x}^{2}}+2x+1+1={{\left( x+1 \right)}^{2}}+1.\)
Vì \({{\left( x+1 \right)}^{2}}\ge 0\,\forall x\Rightarrow {{\left( x+1 \right)}^{2}}+1>0\,\forall x\ne 3\Rightarrow Q+3>0\,\forall x\ne 3.\)
Chọn C