Câu hỏi
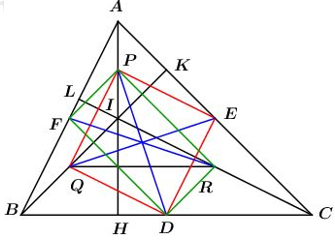
Cho \(\Delta ABC\) có 3 góc nhọn, đường cao AH, BK, CL cắt nhau tại I. Gọi D, E, F là trung điểm của BC, CA, AB. Gọi P, Q, R là trung điểm của IA, IB, IC.
a) Chứng minh: PFDR, PEDQ là hình chữ nhật.
b) Chứng minh: PD, QE, RF cắt nhau tại trung điểm của mỗi đoạn thẳng.
Phương pháp giải:
a) Dựa vào định lý đường trung bình của tam giác để chứng minh được các cạnh PR = DF và \(PR//DF \Rightarrow PFDR\) là hình bình hành theo dấu hiệu nhận biết.
Lại có \(PF//BK;BK \bot AC;AC//PR\) nên \(PF \bot PR\) nên PFDR là hình chữ nhật.
Chứng minh tương tự với tứ giác PQDE.
b) Dựa vào tính chất hình chữ nhật: Hai đường chéo cắt nhau tại trung điểm mỗi đường để suy ra điều phải chứng minh.
Lời giải chi tiết:
a) Xét \(\Delta ABI\) có \(FA = FB\left( {gt} \right);PI = PA\left( {gt} \right) \Rightarrow FP\) là đường trung bình của \(\Delta ABI\)
\( \Rightarrow FP//BI\left( {t/c} \right) \Rightarrow FP//BK\)
Mà \(BK \bot AC\left( {gt} \right)\) nên \(FP \bot AC\left( 1 \right)\)
Xét \(\Delta AIC\) có \(PA = PI\left( {gt} \right);RI = RC\left( {gt} \right) \Rightarrow PR\) là đường trung bình của tam giác
\( \Rightarrow PR//AC;PR = {1 \over 2}AC\left( {t/c} \right)\left( 2 \right)\)
Từ (1) và (2) suy ra \(FP \bot PR\) (từ vuông góc đến song song)
Xét \(\Delta ABC\) có \(FB = FA\left( {gt} \right);DB = DC\left( {gt} \right) \Rightarrow DF\) là đường trung bình của tam giác
Từ (2) và (3) ta có \(PR//DF;PR = DF\) nên PRDF là hình bình hành.
Lại có \(PF//BK;BK \bot AC;AC//PR\) nên \(PF \bot PR\) nên hình bình hành là hình chữ nhật.
Chứng minh tương tự ta cũng có:
\(\left\{ \matrix{PE//CL \cr CL \bot AB \cr AB//PQ \cr} \right. \Rightarrow PE \bot PQ\) và \(PQ//DE//AB;PQ = DE = {1 \over 2}AB\) nên PEDQ là hình bình hành.
Do đó PEDQ là hình chữ nhật.
b) PEDQ là hình chữ nhật nên PD cắt EQ tại trung điểm O của PD và EQ
Lại có PFDR là hình chữ nhật nên PD cắt FR tại trung điểm O của pD và FR
Do đó O là trung điểm các đoạn thẳng \(PD,FR,EQ\)
Vậy ba đường thẳng \(PD,FR,EQ\) cắt nhau tại trung điểm của mỗi đoạn.