Phương pháp giải:

Phương pháp:

Câu 1:

+) Thay giá trị của m đã cho vào hàm số.

+) Tìm ít nhất hai điểm thuộc đồ thị hàm số, sau đó vẽ đường thẳng đi qua hai điểm vừa tìm ta được đồ thị hàm số.

Câu 2:

+) Cho hai đồ thị hàm số: \({{d}_{1}}:\,\,\,y={{a}_{1}}x+{{b}_{1}};\,\,\,{{d}_{2}}:\,\,\,y={{a}_{2}}x+{{b}_{2}}\). Ta có:\({{d}_{1}}//{{d}_{2}}\Leftrightarrow \left\{ \begin{align}  & {{a}_{1}}={{a}_{2}} \\  & {{b}_{1}}\ne {{b}_{2}} \\ \end{align} \right..\)

Câu 3:

+) Khoảng cách từ O đến đường thẳng AB là đường cao OH của tam giác OAB vuông tại O. Sử dụng công thức hệ thức lượng trong tam giác vuông để tính chiều cao của tam giác vuông.

Lời giải chi tiết:

Giải:

1) Vẽ đồ thị hàm số với \(m=2.\)

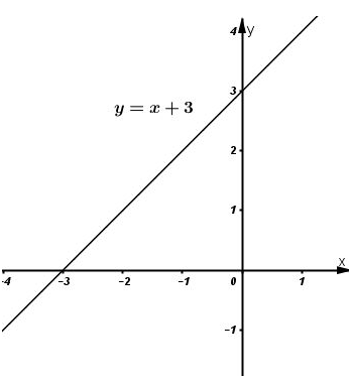
Khi \(m=2\) ta có hàm số: \(y=x+3.\)

Ta có  bảng giá trị:

Đồ thị hàm số:

2) Ta có đường thẳng (1) song song với đường thẳng 

\(y = 2x + 1 \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\m + 1 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 3\\m \ne 0\end{array} \right. \Leftrightarrow m = 3.\)

Vậy với \(m=3\) thì đồ thị hàm số (1) song song với đường thẳng \(y=2x+1.\)

3) Ta có khoảng cách từ O đến đường thẳng \(d:\,\,\,y=2x+4\Leftrightarrow 2x-y+4=0\) là \(OH\).

Áp dụng công thức hệ thức lượng trong tam giác vuông OAB có

đường cao OH ta có:

\(\begin{align}&\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{{{4}^{2}}}+\frac{1}{{{\left( -2 \right)}^{2}}}=\frac{5}{16}\Rightarrow O{{H}^{2}}=\frac{16}{5} \\  & \Rightarrow OH=\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{5}. \\ \end{align}\)

Vậy khoảng cách từ O đến đường thẳng \(y=2x+4\)

là \(d=\frac{4\sqrt{5}}{5}\) (đvđd).