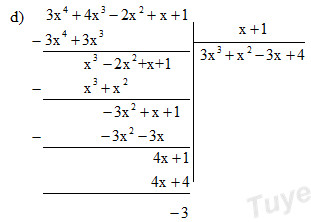Câu hỏi
Thực hiện phép tính:
\(\eqalign{& a)\;3xyz\left( {2{x^2} - 3y - 3} \right) \cr & c)\;{\left( {x + 3} \right)^2} + {\left( {x - 3} \right)^2} - 2\left( {x + 3} \right)\left( {x - 3} \right) + xy \cr} \) \(\eqalign{ & b)\;\left( {6{x^4} - 3{x^3} + {x^2}} \right):\left( {{x^2}} \right) \cr & d)\;\left( {3{x^4} + 4{x^3} - 2{x^2} + x + 1} \right):\left( {x + 1} \right) \cr} \)
Phương pháp giải:
- Thực hiện phép tính bằng cách phối hợp các cách nhân, chia, cộng, trừ đa thức và đơn thức.
Lời giải chi tiết:
\(\begin{array}{l}
a)\;3xyz\left( {2{x^2} - 3y - 3} \right)\\
= 3xyz.2{x^2} - 3xyz.3y - 3xyz.3\\
= 6{x^3}yz - 9x{y^2}z - 9xyz\\
b)\;\left( {6{x^4} - 3{x^3} + {x^2}} \right):\left( {{x^2}} \right)\\
= \left( {6{x^4}} \right):\left( {{x^2}} \right) - \left( {3{x^3}} \right):\left( {{x^2}} \right) + {x^2}:{x^2}\\
= 6{x^2} - 3x + 1\\
c)\;{\left( {x + 3} \right)^2} + {\left( {x - 3} \right)^2} - 2\left( {x + 3} \right)\left( {x - 3} \right) + xy\\
= \left( {{{\left( {x + 3} \right)}^2} - 2\left( {x + 3} \right)\left( {x - 3} \right) + {{\left( {x - 3} \right)}^2}} \right) + xy\\
= {\left( {x + 3 - x + 3} \right)^2} + xy\\
= {6^2} + xy = 36 + xy.
\end{array}\)