Câu hỏi
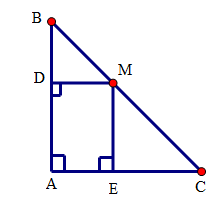
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
- A 6cm
- B 36cm
- C 9cm
- D 12cm
Phương pháp giải:
+ Trước hết ta chứng minh ADME là hình chữ nhật dựa vào dấu hiệu tứ giác có 3 góc vuông là hình chữ nhật.
+ Chứng minh tam giác BDM vuông cân tại D để suy ra BD = DM.
+ Tính chu vi ADME thông độ dài cạnh tam giác vuông cân.
Lời giải chi tiết:
Xét tứ giác ADME có \(\widehat A = \widehat E = \widehat D = {90^ \circ }\) nên ADME là hình chữ nhật.
Xét tam giác DMB có \(\widehat B = {45^ \circ }\) (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó DM = BD.Do ADME là hình chữ nhật nên chu vi ADME là: (AD + DM).2= (AD+BD).2=6.2=12(cm)Vậy chu vi ADME là 12cm