Câu hỏi
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông, thể tích bằng V. Một khối nón có đỉnh là tâm của hình vuông ABCD, có đáy là hình tròn ngoại tiếp tứ giác A’B’C’D’. Tính thế tích khối nón
- A \(\frac{\pi }{4}V\).
- B \(\frac{\pi }{2}V\).
- C \(\frac{\pi }{12}V\).
- D \(\frac{\pi }{6}V\)
Phương pháp giải:
Tính chiều cao và bán kính đáy hình nón
Lời giải chi tiết:
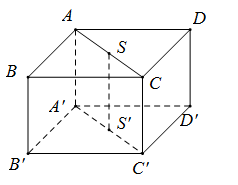
Tâm của hình vuông ABCD và A’B’C’D’ lần lượt là S , S’
Hình nón đã cho có đỉnh là S, chiều cao h = SS’ và bán kính đáy
\(R=S'A'=\frac{A'C'}{2}=\frac{AB\sqrt{2}}{2}\).
Thể tích khối nón:
\({{V}_{1}}=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi \frac{A{{B}^{2}}}{2}h=\frac{\pi }{6}.A{{B}^{2}}h=\frac{\pi }{6}.V\)
Chọn đáp án D
Câu hỏi trước
