Câu hỏi
(1 điểm) Cho tam giác \(ABC\) cân tại \(A\). Gọi \(D,E\) theo thứ tự thuộc các cạnh bên \(AB,AC\) sao cho \(AD{\text{ }} = {\text{ }}AE\) .
a) Tứ giác \(BDEC\) là hình gì? Vì sao?
b) Tính các góc của hình thang \(BEDC\) , biết \(A = {70^o}\) .
- A \(55^0;55^0;125^0;125^0\)
- B \(45^0;45^0;135^0;135^0\)
- C \(45^0;45^0;145^0;145^0\)
- D \(55^0;55^0;135^0;135^0\)
Lời giải chi tiết:
Hướng dẫn giải chi tiết:
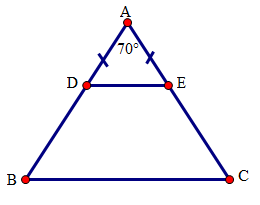
a) Tam giác \(ADE\) có \(AD = AE(gt)\) nên tam giác \(ADE\) cân tại \(A\).
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác \(ABC\) cân tại \(A\) (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra \(DE\parallel BC\)
Tứ giác \(BDEC\) có \(DE // BC\) nên tứ giác \(BDEC\) là hình thang
b) Ta có : \(\hat A = 70^\circ \)
Theo ý a) suy ra:
\(\begin{array}{l}\widehat {ADE} = \widehat {AED}\widehat { = ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {DAE}} \right):2\\ = (180^\circ - 70^\circ ):2\\ = 55^\circ \;\;\;\;\;\;\;\;\;\;\;\;\;\end{array}\)
Vì \(\widehat {BDE}\) và \(\widehat {ADE}\) là hai góc kề bù nên
\(\widehat {BDE} = 180^\circ - \widehat {ADE} = 180^\circ - 55^\circ = 125^\circ \)
Mặt khác,\(\widehat {DEA}\) và \(\widehat {DEC}\) là hai góc kề bù nên
\(\widehat {DEC} = 180^\circ - \widehat {DEA} = 180^\circ - 55^\circ = 125^\circ \)







