Câu hỏi
(1 điểm) Cho tứ giác \(ABCD\) có \(BC = CD\) và \(DB\) là tia phân giác của góc \(D\). Chứng minh rằng \(ABCD\) là hình thang.
- A \(ABCD\) là hình thang
- B \(ABCD\) là hình vuông
- C \(ABCD\) là hình chữ nhật
- D \(ABCD\) là hình thang vuông
Lời giải chi tiết:
Hướng dẫn giải chi tiết:
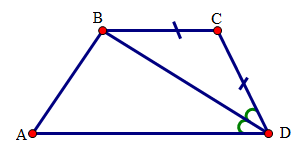
Xét \(\Delta BCD\) có \(BC = CD(gt)\) nên \(\Delta BCD\) là tam giác cân.
Suy ra \(\widehat {CBD} = \widehat {CDB}\)
Vì \(DB\) là tia phân giác góc \(D\) của tứ giác \(ABCD\) nên \)\widehat {ADB} = \widehat {CDB}\)
Do đó \(\widehat {CBD} = \widehat {ADB}\)
Mà hai góc \(\widehat {CBD}\) và \(\widehat {ADB}\) là hai góc ở vị trí so le trong nên suy ra \(BC//AD\) .
Tứ giác \(ABCD\) có \(AD//BC\) (cmt) nên là hình thang.
Câu hỏi trước
