Câu hỏi
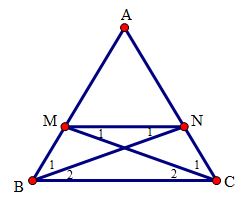
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a) Tứ giác BMNC là hình gì? Vì sao?
b) Tính các góc của tứ giác BMNC biết \(\widehat{A}={{40}^{\circ }}\)?
c) Các điểm M, N ở vị trí nào để BM = MN = NC?
- A a) Hình thang cân.
b) \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\).
c) BN và CM là các đường phân giác của tam giác ABC.
- B a) Hình thang cân.
b) \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\).
c) BN và CM là các đường trung tuyến của tam giác ABC.
- C a) Hình thang cân.
b) \(\widehat{BMN}=\widehat{MNC}={{100}^{0}}\), \(\widehat{B}=\widehat{C}={{80}^{0}}\).
c) BN và CM là các đường phân giác của tam giác ABC.
- D a) Hình thang cân.
b) \(\widehat{BMN}=\widehat{MNC}={{100}^{0}}\), \(\widehat{B}=\widehat{C}={{80}^{0}}\).
c) BN và CM là các đường trung tuyến của tam giác ABC.
Lời giải chi tiết:
a) Ta có: AB = AM + MB
AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A)
BM = NC ( gt)
Suy ra AN = AM
Xét tam giác AMN có: AM = AN (cmt)
Suy ra tam giác AMN cân tại A. Suy ra \(\widehat{AMN}=\widehat{ANM}\)
Xét tam giác ANM có: \(\widehat{A}+\widehat{AMN}+\widehat{ANM}={{180}^{0}}\) (tổng ba góc trong một tam giác)
\(\widehat{AMN}=\frac{{{180}^{0}}-\widehat{A}}{2}\) ( vì \(\widehat{AMN}=\widehat{ANM}\) ) (1)
Xét tam giác ABC cân tại A ta có: \(\widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}\) (tổng ba góc trong một tam giác)
\(\widehat{B}=\frac{{{180}^{0}}-\widehat{A}}{2}\) ( vì \(\widehat{B}=\widehat{C}\)) (2)
Từ (1) và (2) \(\widehat{AMN}=\widehat{B}\)
Mà \(\widehat{AMN},\widehat{B}\) là hai góc đồng vị nên MN // BC.
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có \(\widehat{B}=\widehat{C}\) (\(\Delta ABC\) cân tại A) nên MNCB là hình thang cân.
b. Ta có \(\widehat{B}=\frac{{{180}^{0}}-\widehat{A}}{2}=\frac{{{180}^{0}}-{{40}^{0}}}{2}={{70}^{0}}\)
Ta có : \(\widehat{B}+\widehat{BMN}={{180}^{0}}\) (hai góc trong cùng phía)
\(\widehat{BMN}={{180}^{0}}-\widehat{B}={{180}^{0}}-{{70}^{0}}={{110}^{0}}\)
Do \(BMNC\) là hình thang cân nên \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\)
Vậy \(\widehat{BMN}=\widehat{MNC}={{110}^{0}}\), \(\widehat{B}=\widehat{C}={{70}^{0}}\).
c. Ta có BM = MN khi và chỉ khi \(\widehat{{{N}_{1}}}=\widehat{{{B}_{1}}}={{70}^{0}}\)
\(\Leftrightarrow \widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}\) (vì \(\widehat{{{N}_{1}}}=\widehat{{{B}_{2}}}\))
Tương tự MN = NC khi và chỉ khi \(\widehat {{M_1}} = \widehat {{C_1}} \Leftrightarrow \widehat {{C_1}} = \widehat {{C_2}}\,\,\,\left( {do\,\,\,\widehat {{M_1}} = \widehat {{C_2}}} \right)\)
Như vậy, nếu BN và CM là các đường phân giác của tam giác ABC thì BM = MN = CN.