Câu hỏi
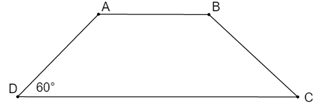
Tìm số đo góc B, biết tứ giác ABCD (AB//CD) là hình thang cân và \(\angle {\rm{D}} = 60^\circ \)
- A \(\angle {\rm{B}} = 60^\circ \)
- B \(\angle {\rm{B}} = 110^\circ \)
- C \(\angle {\rm{B}} = 120^\circ \)
- D \(\angle {\rm{B}} = 80^\circ \)
Phương pháp giải:
Hình thang cân là hình thang có hai góc kề đáy bằng nhau.
Lời giải chi tiết:
Ta có ABCD là hình thang cân nên \(\angle {\rm{A}} = \angle {\rm{B}}\,\,\,\left( 1 \right)\) (tính chất hình thang cân)
Mà \(\angle {\rm{A}} + \angle {\rm{B}} + \angle {\rm{C}} + \angle {\rm{D}} = 360^\circ \)
\( \Rightarrow \angle {\rm{A}} + \angle {\rm{B}} = {360^0} - \left( {\angle C + \angle D} \right)\) \( = {360^0} - {2.60^0} = 240^\circ \,\,\,\,\left( 2 \right)\)
Từ (1), (2) ta kết luận \(\angle {\rm{A = }}\angle {\rm{B}} = 120^\circ \)
Chọn C.