Câu hỏi
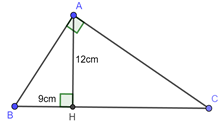
Cho tam giác \(ABC\) vuông tại \(A\), kẻ đường cao \(AH\). Biết \(AH = 12cm,BH = 9cm\). Tính diện tích tam giác\(ABC\).
- A \(60cm^2\)
- B \(72cm^2\)
- C \(78cm^2\)
- D \(80cm^2\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông để tính cạnh \(HC \Rightarrow BC.\)
Khi đó ta có: \({S_{ABC}} = \frac{1}{2}AH.BC.\)
Lời giải chi tiết:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{H^2} = BH.CH\)\( \Leftrightarrow {12^2} = 9.C{H^2}\)\( \Leftrightarrow C{H^2} = 16\) \( \Leftrightarrow CH = 4\left( {cm} \right)\)
Ta có: \(BC = BH + CH = 9 + 4 = 13\left( {cm} \right)\)
\( \Rightarrow {S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.12.13 = 78\,\,\,\left( {c{m^2}} \right)\)
Chọn C.