Phương pháp giải:

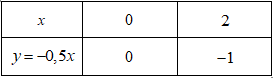
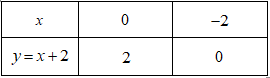
a) Lập bảng giá trị các điểm đi qua của mỗi đồ thị hàm số và vẽ đồ thị.

b) Sử dụng \(d//d'\) thì \(a = a',b \ne b'\).

Lời giải chi tiết:

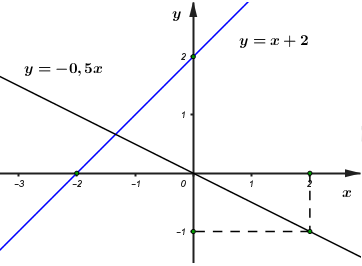
a) Vẽ đồ thị \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)

Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\)

Bảng giá trị \(y =  - 0,5x\)

Bảng giá trị \(y = x + 2\)

Đồ thị:

b) Xác định hệ số \(a,b\) của đường thẳng \(\left( d \right):y = ax + b\) biết rằng \(\left( d \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( d \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ là \( - 3\).

Vì \(\left( d \right)//\left( {{d_1}} \right)\) nên \(a =  - 0,5\) và \(b \ne 0.\) Khi đó \(\left( d \right):y =  - 0,5x + b\)

Gọi \(A\left( {{x_0}; - 3} \right)\) là tọa độ giao điểm của \(\left( d \right)\) và \(\left( {{d_2}} \right)\)

+\(A\left( {{x_0}; - 3} \right) \in \left( {{d_2}} \right)\) \( \Rightarrow  - 3 = {x_0} + 2 \Rightarrow {x_0} =  - 5\)

+\(A\left( { - 5; - 3} \right) \in \left( d \right)\) \( \Rightarrow  - 3 =  - 0,5.\left( { - 5} \right) + b\) \( \Rightarrow b =  - 5,5\) (TMĐK)

Vậy \(\left( d \right):y =  - 0,5x - 5,5\)

Chọn C.