Câu hỏi
Chọn đáp án đúng nhất:
Câu 1:
a) Tìm \(x\) biết: \(4x + 2 = 0\)
b) Rút gọn: \(A = \left( {\sqrt 5 - 3} \right)\left( {\sqrt 5 + 3} \right) + 6\)
- A \(\begin{array}{l}{\rm{a)}}\,\,x = \frac{1}{2}\\{\rm{b)}}\,\,A = 1\end{array}\)
- B \(\begin{array}{l}{\rm{a)}}\,\,x = - \frac{1}{2}\\{\rm{b)}}\,\,A = - 2\end{array}\)
- C \(\begin{array}{l}{\rm{a)}}\,\,x = - \frac{1}{2}\\{\rm{b)}}\,\,A = 2\end{array}\)
- D \(\begin{array}{l}{\rm{a)}}\,\,x = \frac{1}{2}\\{\rm{b)}}\,\,A = - 1\end{array}\)
Phương pháp giải:
a) Giải phương trình bậc nhất một ẩn.
b) Sử dụng công thức hằng đẳng thức để rút gọn biểu thức.
Lời giải chi tiết:
a)\(4x + 2 = 0 \Rightarrow 4x = - 2 \Rightarrow x = \frac{{ - 2}}{4} = \frac{{ - 1}}{2}\)
Vậy \(x = - \frac{1}{2}.\)
b) \(A = \left( {\sqrt 5 - 3} \right)\left( {\sqrt 5 + 3} \right) + 6\)
\(\begin{array}{l}A = {\left( {\sqrt 5 } \right)^2} - {3^2} + 6\\A = 5 - 9 + 6\\A = 2.\end{array}\)
Vậy \(A = 2.\)
Chọn C.
Câu 2:
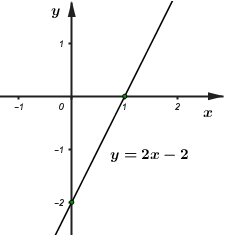
Cho đường thẳng (d): \(y = 2{\rm{x}} - 2\)
a) Vẽ đường thẳng \(\left( d \right)\) trong hệ trục tọa độ \(Oxy.\)
b) Tìm \(m\) để đường thẳng \(\left( {d'} \right):\,\,y = \left( {m - 1} \right)x + 2m\) song song với đường thẳng \(\left( d \right).\)
- A \({\rm{b)}}\,\,m = 1\)
- B \({\rm{b)}}\,\,m = 2\)
- C \({\rm{b)}}\,\,m = 3\)
- D \({\rm{b)}}\,\,m = - 1\)
Phương pháp giải:
a) Lập bảng giá trị, vẽ đồ thị hàm số.
b) Cho hai đường thẳng \(d:\,\,y = ax + b,\,\,\,\,d':\,\,\,y = a'x + b'.\)
Khi đó: \(d//d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..\)
Lời giải chi tiết:
a) Vẽ đường thẳng \(\left( d \right)\) trong hệ trục tọa độ \(Oxy.\)
Ta có bảng giá trị:
Vậy đường thẳng \(\left( d \right):\,\,\,y = 2x - 2\) cắt trục hoàn tại điểm \(\left( {1;\,\,0} \right)\) và cắt trục tung tại điểm \(\left( {0; - 2} \right).\)
b) Tìm \(m\) để đường thẳng \(\left( {d'} \right):\,\,y = \left( {m - 1} \right)x + 2m\) song song với đường thẳng \(\left( d \right).\)
Để đường thẳng \(\left( {d'} \right):\,\,\,\,y = (m - 1)x + 2m\)song song với đường thẳng \(\left( d \right):\,\,\,y = 2x - 2\)
\( \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\2m \ne - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m = 3\\m \ne - 1\end{array} \right. \Rightarrow m = 3\)
Vậy \(m = 3\)thỏa mãn yêu cầu bài toán.
Chọn C.