Câu hỏi
Cho hàm số \(y = f\left( x \right)\) xác định trên \(R\backslash \left\{ { - 1;\,1} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
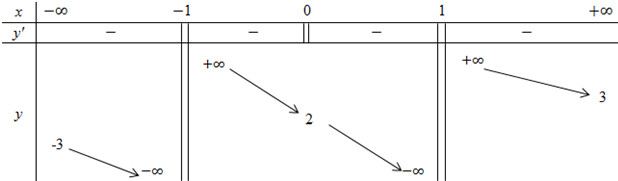
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng \(y = 2m + 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt.
- A \(m \le - 2\) hoặc \(m \ge 1\)
- B \(m \ge 1\)
- C \(m < - 2\) hoặc \(m > 1\)
- D \(m \le - 2\)
Phương pháp giải:
Dựa vào BBT để tìm \(m.\)
Lời giải chi tiết:
Quan sát BBT ta thấy đường thẳng \(y = 2m + 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left[ \begin{array}{l}2m + 1 < - 3\\2m + 1 > 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - 2\\m > 1\end{array} \right.\) .
Chọn C.
Câu hỏi trước
