Câu hỏi
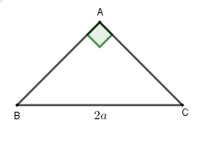
Cho hình nón có thiết diện qua trục là một tam giác vuông cân cạnh huyền bằng \(2a\). Tính diện tích xung quanh \({S_{xq}}\) của hình nón.
- A
\({S_{xq}} = \pi \sqrt 2 {a^2}\)
- B \({S_{xq}} = 2\pi \sqrt 2 {a^2}\)
- C \({S_{xq}} = 2\pi {a^2}\)
- D \({S_{xq}} = \pi {a^2}\)
Phương pháp giải:
Diện tích xung quanh \({S_{xq}} = \pi rl\).
Lời giải chi tiết:
Bán kính đáy \(r = \dfrac{1}{2}BC = \dfrac{1}{2}.2a = a\).
Tam giác \(ABC\) vuông cân có \(BC = 2a\) nên \(AB = AC = a\sqrt 2 = l\).
Vây diện tích xung quanh \({S_{xq}} = \pi rl = \pi .a.a\sqrt 2 = \pi {a^2}\sqrt 2 \).
Chọn A.
Câu hỏi trước
