Cho mạch điện RLC mắc nối tiếp có biến trở \(R = 10\Omega ,L = \frac{{0,2}}{\pi }\left( H \right),C = \frac{{{{10}^{ - 3}}}}{\pi }\left( F \right)\). Điện áp hai đầu đoạn mạch là \(u = 60\sqrt 2 \cos \left( {10\pi t + \frac{\pi }{3}} \right)\left( V \right)\)
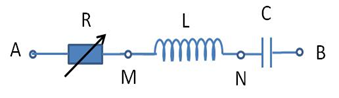
Cho mạch điện RLC mắc nối tiếp có biến trở \(R = 10\Omega ,L = \frac{{0,2}}{\pi }\left( H \right),C = \frac{{{{10}^{ - 3}}}}{\pi }\left( F \right)\). Điện áp hai đầu đoạn mạch là \(u = 60\sqrt 2 \cos \left( {10\pi t + \frac{\pi }{3}} \right)\left( V \right)\)

Điện áp hiệu dụng hai đầu đoạn mạch có giá trị:
Điện áp hiệu dụng hai đầu đoạn mạch có giá trị:
\(60\sqrt 2 V\)
60V
\(120\sqrt 2 V\)
120V
Đáp án: B
Ta có: \(U = \frac{{{U_0}}}{{\sqrt 2 }}\)
Từ phương trình điện áp, ta có:
\({U_0} = 60\sqrt 2 V\)
Điện áp hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }} = \frac{{60\sqrt 2 }}{{\sqrt 2 }} = 60V\)

Tổng trở của đoạn mạch có giá trị:
Tổng trở của đoạn mạch có giá trị:
\(10\sqrt 2 \Omega \)
\(10\Omega \)
\(20\Omega \)
\(20\sqrt 2 \Omega \)
Đáp án: A
Tổng trở của mạch:
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}\)
Ta có:
Điện trở : \(R = 10\Omega \)
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 3}}}}{\pi }}} = 10\Omega \)
Cảm kháng: \({Z_L} = \omega L = 100\pi .\frac{{0,2}}{\pi } = 20\Omega \)
Tổng trở của mạch:
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{10}^2} + {{\left( {20 - 10} \right)}^2}} = 10\sqrt 2 \Omega \)
Biểu thức cường độ dòng điện trong mạch là:
Biểu thức cường độ dòng điện trong mạch là:
\(i = 6\cos \left( {100\pi t + \frac{\pi }{6}} \right)\left( A \right)\)
\(i = 6\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{6}} \right)\left( A \right)\)
\(i = 3\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{{12}}} \right)\left( A \right)\)
\(i = 6\cos \left( {100\pi t + \frac{\pi }{{12}}} \right)\left( A \right)\)
Đáp án: D
Độ lệch pha giữa u và i là:
\(\cos \varphi = \frac{R}{Z} = \frac{{10}}{{10\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = \frac{\pi }{4}\)
Ta có: \(\varphi = {\varphi _u} - {\varphi _i} \Leftrightarrow \frac{\pi }{4} = \frac{\pi }{3} - {\varphi _i}\)
\( \Rightarrow {\varphi _i} = \frac{\pi }{{12}}\)
Lại có: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{60\sqrt 2 }}{{10\sqrt 2 }} = 6A\)
Vậy \(i = 6\cos \left( {100\pi t + \frac{\pi }{{12}}} \right)\left( A \right)\)
Biểu thức hiệu điện thế giữa hai đầu đoạn mạch MB là:
Biểu thức hiệu điện thế giữa hai đầu đoạn mạch MB là:
\({u_{MB}} = 60\cos \left( {100\pi t + \frac{{7\pi }}{{12}}} \right)\left( V \right)\)
\({u_{MB}} = 60\sqrt 2 \cos \left( {100\pi t + \frac{{7\pi }}{{12}}} \right)\left( V \right)\)
\({u_{MB}} = 60\cos \left( {100\pi t - \frac{{7\pi }}{{12}}} \right)\left( V \right)\)
\({u_{MB}} = 60\cos \left( {100\pi t + \frac{\pi }{{12}}} \right)\left( V \right)\)
Đáp án: A
Ta có: \({U_{0MB}} = {I_0}.{Z_{MB}} = 6.\sqrt {{{\left( {20 - 10} \right)}^2}} = 60V\)
Độ lệch pha giữa \({u_{MB}}\) và i là:
\(\cos \varphi ' = \frac{0}{{{Z_L} - {Z_C}}} = 0 \Rightarrow \varphi ' = \frac{\pi }{2}\)
\( \Rightarrow \frac{\pi }{2} = {\varphi _{uMB}} - \frac{\pi }{{12}} \Leftrightarrow {\varphi _{uMB}} = \frac{\pi }{2} + \frac{\pi }{{12}} = \frac{{7\pi }}{{12}}\)
Vậy \({u_{MB}} = 60\cos \left( {100\pi t + \frac{{7\pi }}{{12}}} \right)\left( V \right)\)








Danh sách bình luận