Đề bài
Biểu diễn tập nghiệm của bất phương trình \(x \ge 8\) trên trục số, ta được
-
A.

-
B.

-
C.

-
D.
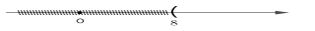
Phương pháp giải
Biểu diễn tập nghiệm trên trục số
Lời giải của GV Loigiaihay.com

Ta biểu diễn \(x \ge 8\) trên trục số như sau:
Đáp án : C







