Đề bài
Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(4\,cm\) (làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(4,702\,cm\)
-
B.
\(4,7\,cm\)
-
C.
\(4,6\,cm\)
-
D.
\(4,72\,cm\)
Phương pháp giải
+ Sử dụng tính mối quan hệ giữa cung và dây cung để tính góc \(AOB\)
+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.
Lời giải của GV Loigiaihay.com
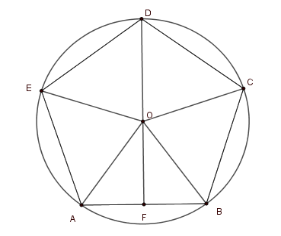
+ Vì \(AB = BC = CD = DE = EA\) nên các cung \(AB,BC,CD,DE,EA\) bằng nhau
Suy ra \(\widehat {AOB} = \dfrac{1}{5}.360^\circ = 72^\circ \)
+) Xét tam giác \(AOB\) cân tại \(O\) có \(OF\) là đường cao cũng là đường phân giác nên \(\widehat {BOF} = 36^\circ \)
Ta có \(FB = OB.\sin \widehat {BOF} = 4.\sin 36^\circ \Rightarrow AB = 2FB = 8\sin 36^\circ \approx 4,7\,cm\)
Đáp án : B
Chú ý
Một số em có thể chọn sai đáp án là A, C do không làm tròn hoặc làm tròn sai.
