Đề bài
Đường tròn nội tiếp hình vuông cạnh \(a\) có bán kính là
-
A.
\(a\sqrt 2 \)
-
B.
\(\dfrac{{a\sqrt 2 }}{2}\)
-
C.
\(\dfrac{a}{2}\)
-
D.
\(\dfrac{{a\sqrt 3 }}{2}\)
Phương pháp giải
+ Sử dụng tính chất của hình vuông
Lời giải của GV Loigiaihay.com
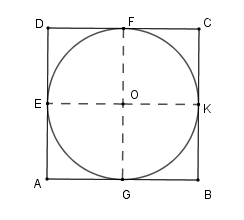
Gọi \(O\) là tâm của hình vuông \(ABCD\) , \(E;\,F;K;\,G\) là trung điểm của \(AD,\,DC,\,BC,\,AB\)
Khi đó ta có \(OE = OF = OK = OG = \dfrac{a}{2}\) . Hay \(O\) là tâm đường tròn nội tiếp hình vuông \(ABCD\) .
Bán kính đường tròn là \(R = \dfrac{a}{2}\) .
Đáp án : C
