Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có $AB = a\sqrt 2 $. Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Tính khoảng cách \(d\) từ \(D\) đến mặt phẳng \(\left( {SBC} \right)\).
-
A.
$d = \dfrac{{a\sqrt {10} }}{2}.$
-
B.
$d = a\sqrt 2 .$
-
C.
$d = \dfrac{{2a\sqrt 3 }}{3}.$
-
D.
$d = \dfrac{{a\sqrt 3 }}{3}.$
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
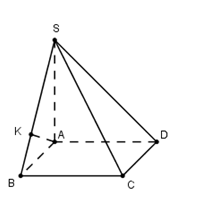
Do AD // BC nên $d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right).$
Gọi K là hình chiếu của A trên SB, suy ra $AK \bot SB\,\,\,\left( 1 \right)$.
Ta có: \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AK \bot \left( {SBC} \right)\)
Khi $d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a\sqrt 3 }}{3}.$
Đáp án : C








Danh sách bình luận