Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(DB'\) bằng
-
A.
\(a\sqrt 2 \).
-
B.
\(\dfrac{{a\sqrt 6 }}{2}\).
-
C.
\(\dfrac{{a\sqrt 3 }}{2}\).
-
D.
\(\dfrac{{a\sqrt 6 }}{3}\).
Phương pháp giải
Kẻ \(AH \bot B'D\) và tính độ dài \(AH\).
Lời giải của GV Loigiaihay.com
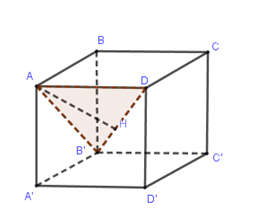
Gọi $H$là chân đường vuông góc hạ từ $A$ xuống $DB'$.
Dễ thấy $AD \bot \left( {ABB'A'} \right) \Rightarrow \Delta ADB'$vuông đỉnh $A$.
Lại có $AD = a;AB' = a\sqrt 2 \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{AB{'^2}}} \Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}$
Đáp án : D







