Xác định hàm số \(y = a{x^2}\) biết rằng đồ thị của hàm số đi qua điểm \(A\left( { - 2;5} \right)\).

Cho parabol \(y=-{{x}^{2}}\). Vẽ đường thẳng song song với trục hoành cắt trục tung tại điểm \(-5\) và cắt parabol tại \(M\) và \(N\). Diện tích tam giác \(OMN\) là

Cho hàm số \(y = 2{x^2}\).

a) Hoàn thành bảng giá trị sau vào vở:

b) Trong mặt phẳng Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;2{x^2}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị của hàm số \(y = 2{x^2}\).

Vẽ đồ thị của các hàm số sau:

a) \(y = 3{x^2}\);

b) \(y =  - \frac{1}{3}{x^2}\).

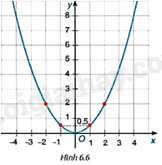
Biết đường cong trong Hình 6.6 là một parabol \(y = a{x^2}\).

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x =  - 2\).

c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).

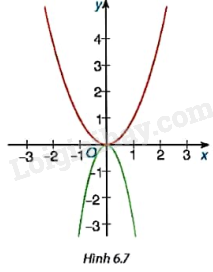
Trong Hình 6.7 có hai đường cong là đồ thị của hai hàm số \(y =  - 3{x^2}\) và \(y = {x^2}\). Hãy cho biết đường nào là đồ thị của hàm số \(y =  - 3{x^2}\).

Điểm nào sau đây thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?

A. \(\left( {1;2} \right)\).

B. \(\left( {2;1} \right)\).

C. \(\left( { - 1;2} \right)\).

D. \(\left( { - 1;\frac{1}{2}} \right)\).

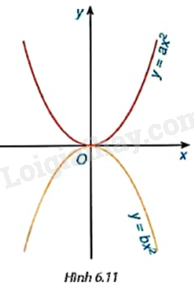
Hình 6.11 là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?

A. \(a < 0 < b\).

B. \(a < b < 0\).

C. \(a > b > 0\).

D. \(a > 0 > b\).

Vẽ đồ thị của các hàm số \(y = \frac{5}{2}{x^2}\) và \(y =  - \frac{5}{2}{x^2}\) trên cùng một mặt phẳng tọa độ.

Biết rằng parabol \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {2;4\sqrt 3 } \right)\).

a) Tìm hệ số a và vẽ đồ thị của hàm số \(y = a{x^2}\) với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x =  - 1\).

c) Tìm các điểm thuộc parabol có tung độ \(y = 5\sqrt 3 \).

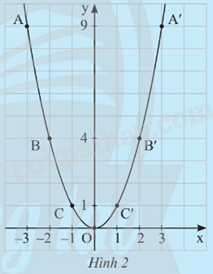
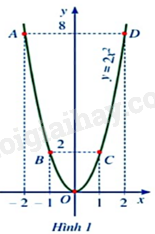
Cho hàm số \(y = {x^2}\). Ta lập bảng giá trị sau:

Từ bảng trên, ta lấy các điểm A(-3;9), B(-2;4), C(-1;1), O(0;0), C’(1;1), B’(2;4), A’(3;9) trên mặt phẳng tọa độ Oxy. Đồ thị của hàm số \(y = {x^2}\) là một đường cong đi qua các điểm nêu trên và có dạnh như Hình 2.

Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:

a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?

b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và C’ so với trục tung?

c) Điểm nào là điểm thấp nhất của đồ thị?

Cho hàm số \(y =  - \frac{3}{2}{x^2}\).

a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị -2; -1;0;1;2.

b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị của hàm số đó?

Vẽ đồ thị hàm số y = 2x².

Cho hai hàm số \(y = \frac{1}{4}{x^2}\)và \(y =  - \frac{1}{4}{x^2}\). Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.

Cho hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).

a) Tìm a, biết đồ thị của hàm số đi qua điểm M(2;6).

b) Vẽ đồ thị của hàm số với a vừa tìm được.

c) Tìm các điểm thuộc đồ thị trên có tung độ y = 9.

Kết luận nào sau đây đúng khi nói về đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)?

A. Với a > 0, đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị.

B. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.

C. Với a > 0, đồ thị nằm phía dưới trục hoành và O là điểm thấp nhất của đồ thị.

D. Với a < 0, đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.

Điểm nào sau đây thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\)?

A. (4;4)

B. (-4;8)

C. (-4;-8)

D. (4;-4)

Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm A(2; -2). Giá trị của a bằng

A. 2

B. - 2

C. \(\frac{1}{2}\)

D. \( - \frac{1}{2}\)

Cho hai hàm số \(y = \frac{3}{2}{x^2}\) và \(y =  - {x^2}\). Vẽ đồ thị của hai hàm số đã cho trên cùng mặt phẳng tọa độ Oxy.

Cho hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).

a) Tìm a, biết đồ thị của hàm số đi qua điểm M(2;2).

b) Vẽ đồ thị (P) của hàm số với a vừa tìm được.

c) Tìm các điểm thuộc đồ thị (P) trên có tung độ y = 8.

a)   Nêu khái niệm đồ thị của hàm số \(y = f(x)\).

b)  Xét hàm số \(y = 2{x^2}\). Hãy thực hiện các hoạt động sau:          

- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau: 

- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.

- Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y = 2{x^2}\).

c)   Xét hàm số \(y =  - 2{x^2}\). Hãy thực hiện các hoạt động sau:

- Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

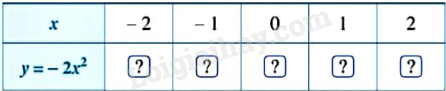
- Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.

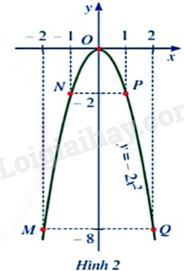
- Quan sát Hình 2, vẽ vẽ đường cong như ở Hình 2 đi qua 5 điểm M, N, O, P, Q. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số \(y =  - 2{x^2}\).

Vẽ đồ thị của hàm số \(y =  - 3{x^2}\)

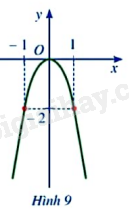
Giả sử đồ thị của hàm số \(y = a{x^2}(a \ne 0)\) là parabol ở Hình 9. Giá trị của a bằng:

A. 2

B. \( - 2\)        

C. \(\frac{1}{2}\)

D. \(\frac{{ - 1}}{2}\)

Cho hàm số \(y = \frac{{ - 2}}{3}{x^2}\).

a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

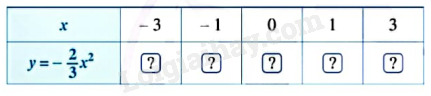
b) Dựa vào bảng trên, vẽ đồ thị của hàm số.

Quan sát đồ thị của hai hàm số \(y = \frac{1}{2}{x^2}\) (Hình 6.1a) và \(y =  - \frac{1}{2}{x^2}\) (Hình 6.1b).

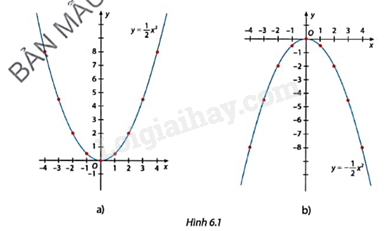
Với mỗi đồ thị, hãy đồ thị:

a) Đồ thị nằm phía trên hay phía dưới trục hoành;

b) Điểm thấp nhất hoặc điểm cao nhất của đồ thị;

c) Mối liên hệ giữa tung độ của hai điểm có hoành độ đối nhau thuộc đồ thị;

d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy có trùng nhau hay không.

Vẽ đồ thị y = -2x².

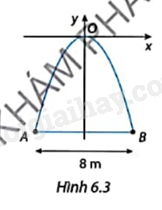
Một cổng chào được thiết kế theo hình parabol là một phần của đồ thị hàm số \(y =  - \frac{{{x^2}}}{2}\). Khoảng cách giữa hai chân cổng là AB = 8 m (Hình 6.3).

a) Tìm hoành độ của hai điểm A, B.

b) Tìm chiều cao của cổng.

Cho hàm số y = - x².

a) Vẽ đồ thị hàm số.

b) Tìm trên đồ thị những điểm có tung độ bằng -4

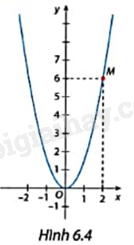
Cho hàm số y = ax² có đồ thị là đường parabol như Hình 6.4

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc đồ thị có hoành độ bằng -1.

c) Tìm các điểm thuộc đồ thị có tung độ bằng \(\frac{2}{3}\).

Đồ thị hàm số y = \(\frac{1}{4}\)x² không đi qua điểm

A. M(2;1)

B. N(-2;1)

C. P(-4;4)

D. Q(4;1)

Hình 6.11 là đồ thị hàm số y = f(x) = ax² (a\( \ne \)0). Giá trị của a bằng

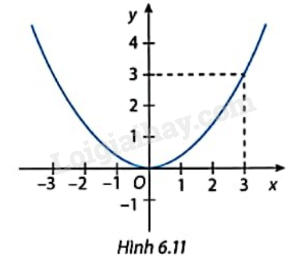
A. 3

B. \(\frac{1}{3}\)

C. 1

D. \(\frac{1}{2}\)