Cho đường tròn $(O;R)$. Cát tuyến qua $A$ ở ngoài $(O)$ cắt $(O)$ tại $B$ và $C$. Cho biết $AB = BC$ và kẻ đường kính $COD$. Tính độ dài đoạn thẳng $AD.$
-
A.
$AD = R$
-
B.
$AD = 3R$
-
C.
$AD = \dfrac{R}{2}$
-
D.
$AD = 2R$
+) Nhắc lại : Cát tuyến là đường thẳng cắt đường tròn tại hai điểm.
+) Sử dụng Pytago để tính toán.
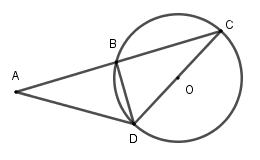
Xét $\left( O \right)$ có $OB = OC = OD$$ \Rightarrow BO = \dfrac{{DC}}{2}$$ \Rightarrow \Delta BDC$ vuông tại $B$ (tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)
Suy ra $BD \bot AC$.
Xét $\Delta ADC$ có $BD$ vừa là đường trung tuyến vừa là đường cao nên $\Delta ADC$ cân tại $D \Rightarrow DA = DC = 2R$
Vậy $AD = 2R.$
Đáp án : D
Các bài tập cùng chuyên đề
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
Nếu đường thẳng $d$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ thì
Cho đường tròn $\left( O \right)$ và đường thẳng $a$. Kẻ $OH \bot a$ tại $H$, biết $OH > R$ khi đó đường thẳng $a$ và đường tròn $\left( O \right)$
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
Cho đường tròn tâm $O$ bán kính $3cm$ và một điểm $A$ cách $O$ là $5cm$. Kẻ tiếp tuyến $AB$ với đường tròn ( $B$ là tiếp điểm). Tính độ dài $AB$.
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
Cho hai đường thẳng $a$ và $b$ song song với nhau, cách nhau một khoảng là $h$. Một đường tròn $\left( O \right)$ tiếp xúc với $a$ và $b$. Hỏi tâm $O$ di động trên đường nào?
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
