Cho tứ diện \(ABCD\) có cạnh $AB$, $BC$, $CD$ bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
-
A.
Góc giữa \(AC\) và \(\left( {BCD} \right)\) là góc \(ACB\).
-
B.
Góc giữa \(AD\) và \(\left( {ABC} \right)\) là góc \(ADB\).
-
C.
Góc giữa \(AC\) và \(\left( {ABD} \right)\) là góc \(CAB\).
-
D.
Góc giữa \(CD\) và \(\left( {ABD} \right)\) là góc \(CBD\).
- Tìm hình chiếu của \(A,C\) lên mặt phẳng \(\left( {BCD} \right)\) rồi suy ra góc cần tìm.
- Góc (không vuông) giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Từ giả thiết ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right)\).
Do đó \(\left( {AC,\left( {BCD} \right)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\).
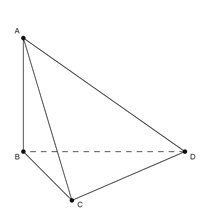
Đáp án : A
Một số em có thể hiểu nhầm góc giữa AC và (ABD) bằng \(\widehat {CAB}\) và chọn C là sai do CB không vuông góc với BD nên CB không vuông góc với (ABD).
Từ đó AB không thể là hình chiếu của AC lên (ABD) dẫn tới góc giữa AC và (ABD) không bằng góc giữa AC với AB và không phải góc \(\widehat {CAB}\)








Danh sách bình luận