Đề bài
Cho tứ diện \(ABCD\) có \(AB \bot CD\) và \(AC \bot BD\). Gọi \(H\) là hình chiếu vuông góc của \(A\) lên \(mp(BCD)\). Các khẳng định sau, khẳng định nào sai?
-
A.
\(H\) là trực tâm tam giác \(BCD\).
-
B.
\(CD \bot (ABH)\).
-
C.
\(AD \bot BC\).
-
D.
Các khẳng định trên đều sai.
Lời giải của GV Loigiaihay.com
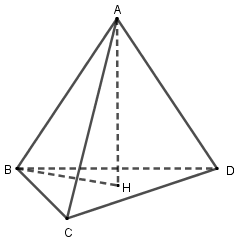
Ta có \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot (ABH) \Rightarrow CD \bot BH\). Tương tự \(BD \bot CH\)
Suy ra \(H\) là trực tâm \(\Delta BCD\). Suy ra đáp án A, B đúng.
Ta có \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot DH\end{array} \right. \Rightarrow BC \bot AD\), suy ra C đúng.
Đáp án : D
Chú ý
Từ nay các em có thể coi đây như một tính chất để sử dụng : Tứ diện có hai cặp cạnh đối vuông góc thì cặp cạnh đối còn lại cũng vuông góc.
