Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên \(mp(ABC)\). Mệnh đề nào sai trong các mệnh đề sau:
-
A.
\(H\) là trực tâm \(\Delta ABC\).
-
B.
\(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
-
C.
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
-
D.
\(CH\) là đường cao của \(\Delta ABC\).
Chứng minh \(H\) là trực tâm tam giác \(ABC\).
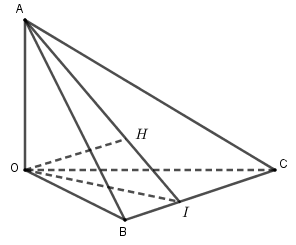
Ta có \(OA \bot (OBC) \Rightarrow OA \bot BC,\) mà \(OH \bot BC\) \( \Rightarrow BC \bot (OAH) \Rightarrow BC \bot AH\).
Tương tự, ta có \(AB \bot CH\), suy ra đáp án A, D đúng.
Ta có \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{I^2}}} \) \(= \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
với \(I = AH \cap BC\), suy ra đáp án C đúng.
Đáp án : B
Sau này các em có thể coi đây như một tính chất cần nhớ để sử dụng :
Trong tứ diện vuông (ba cạnh tại một đỉnh vuông góc với nhau), hình chiếu của đỉnh đó lên mặt đối diện là trực tâm của tam giác đó.
