Cho tam giác đều $ABC$ cạnh bằng $a$ , các đường cao là $BM$ và $CN$ . Gọi $D$ là trung điểm cạnh $BC$ .

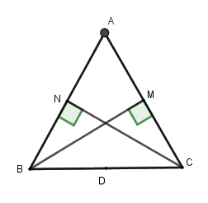
Gọi $D$ là trung điểm $BC$.

Xét hai tam giác vuông $BNC$ và $BMC$ có $ND,MD$ là hai đường trung tuyến

$ \Rightarrow DN = DB = DC = DM = \dfrac{{BC}}{2}$ nên bốn điểm $B,N,M,C$ cùng thuộc đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.

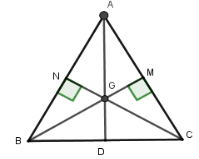
Từ câu trước ta xác định vị trí tương đối của  điểm $G$ với đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.

Gọi cạnh của tam giác đều $ABC$ là $a$.$\left( {a > 0} \right)$

Ta có $G$ là trực tâm $\Delta ABC$ nên $G$ cũng là trọng tâm $\Delta ABC$ suy ra $GD = \dfrac{1}{3}AG$.

$D$ là trung điểm $BC \Rightarrow AD \bot BD$; $DC = \dfrac{{BC}}{2} = \dfrac{a}{2}$

Theo định lý Pytago cho tam giác vuông $ADC$ ta có $AD = \sqrt {A{C^2} - D{C^2}}  = \dfrac{{a\sqrt 3 }}{2}$$ \Rightarrow GD = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}$

Nhận thấy $GD = \dfrac{{a\sqrt 3 }}{6} < \dfrac{a}{2} = \dfrac{{BC}}{2}$ nên điểm $G$ nằm trong đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.

Và $AD = \dfrac{{a\sqrt 3 }}{2} > \dfrac{a}{2} = \dfrac{{BC}}{2}$ nên điểm $A$ nằm ngoài đường tròn tâm $D$ bán kính $\dfrac{{BC}}{2}$.