Đề bài
Cho tam giác $ABC$ vuông tại $A$ , có$AB = 15cm;AC = 20cm$. Tính bán kính đường tròn ngoại tiếp tam giác $ABC.$
-
A.
$R = 25$
-
B.
$R = \dfrac{{25}}{2}$
-
C.
$R = 15$
-
D.
$R = 20$
Phương pháp giải
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Sử dụng định lý Pytago để tính toán
Lời giải của GV Loigiaihay.com
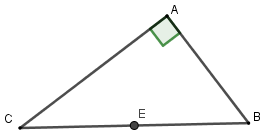
Vì tam giác $ABC$ vuông tại$A$ nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền $BC$, bán kính là $R = \dfrac{{BC}}{2}$.
Theo định lý Pytago ta có $BC = \sqrt {A{C^2} + A{B^2}} = 25$ nên bán kính $R = \dfrac{{25}}{2}$.
Đáp án : B







