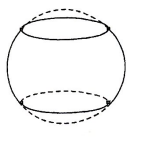
Một thùng rượu vang có dạng hình tròn xoay có hai đáy là hai hình tròn bằng nhau, khoảng cách giữa hai đáy bằng \(80\left( {cm} \right)\). Đường sinh của mặt xung quanh thùng là một phần đường tròn có bán kính \(60\left( {cm} \right)\)(tham khảo hình minh họa bên). Hỏi thùng đó có thể đựng bao nhiêu lít rượu?(làm tròn đến hàng đơn vị)
-
A.
\(771\)
-
B.
\(385\)
-
C.
\(603\)
-
D.
\(905\)
Áp dụng công thức tính chỏm cầu \({V_{cc}} = \pi {h^2}\left( {R - \dfrac{h}{3}} \right)\), với \(R\) là bán khối cầu, h là chiều cao của chỏm cầu.
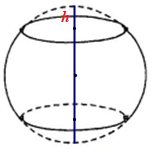
Ta có đường kính mặt cầu là \(60.2 = 120\,\,\,\left( {cm} \right).\)
Mà khoảng cách giữa hai đáy của thùng rượu là \(80cm\)
Nên chiều cao chỏm cầu là \(h = \dfrac{{120 - 80}}{2} = 20\,\,\left( {cm} \right).\)
Thế tích của 1 chỏm cầu chiều cao \(h = 20\) và bán kính \(60cm\)là
\({V_{cc}} = \pi {h^2}\left( {R - \dfrac{h}{3}} \right) = \pi {.20^2}\left( {60 - \dfrac{{20}}{3}} \right) = \dfrac{{64000}}{3}\pi \,\,\left( {c{m^3}} \right) = \dfrac{{64\pi }}{3}\,\,\left( l \right)\)
Thể tích của cả khối cầu bán kính 60 cm là \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.60^3} = 288000\pi \,\,\left( {c{m^3}} \right) = 288\pi \,\,\left( l \right)\)
Khi đó thể tích thùng rượu là \(V' = V - 2{V_{cc}} = \dfrac{{736}}{3}\pi \,\,\left( l \right) \approx 771\,\,\left( l \right).\)
Đáp án : A
Các bài tập cùng chuyên đề
Mặt cầu ngoại tiếp hình đa diện nếu nó:
Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:
Tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:
Hình nào sau đây không có mặt cầu ngoại tiếp?
Số mặt cầu ngoại tiếp tứ diện là:
Hình chóp nào sau đây luôn nội tiếp được mặt cầu?
Cho hình chóp tam giác \(S.ABC\) có \(\widehat {SAC} = \widehat {SBC} = {90^0}\). Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
Tâm mặt cầu ngoại tiếp hình chóp tam giác đều nằm ở đâu?
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên \(b\). Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:
Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
Công thức tính diện tích mặt cầu là:
Khối cầu thể tích \(V\) thì bán kính là:
Ba đoạn thẳng $SA,SB,SC$ đôi một vuông góc tạo với nhau thành một tứ diện $SABC$ với $SA = a,SB = 2a,SC = 3a$ . Tính bán kính mặt cầu ngoại tiếp hình tứ diện đó là
Hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$ có $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và có $SA = a,AB = b,AC = c$. Mặt cầu đi qua các đỉnh $A,B,C,S$ có bán kính $r$ bằng :
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $1$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích $V$ của khối cầu ngoại tiếp hình chóp đã cho.
Cho hình chóp tam giác đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh \(SA = \dfrac{{2a\sqrt 3 }}{3}\) . Gọi $D$ là điểm đối xứng của $B$ qua $C$. Tính bán kính $R$ của mặt cầu ngoại tiếp hình chóp $S.ABD$
Cho tứ diện đều $ABCD$ có cạnh $a$. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\,AD = 2a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\). Tính thể tích khối cầu ngoại tiếp hình chóp \(S.ABCD\).
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông cân đỉnh $A,AB = AC = a,AA' = a\sqrt 2 $. Diện tích mặt cầu ngoại tiếp tứ diện $CA'B'C'$ là:
Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $
