Cho tam giác $ABC$ có các đường cao $BD,CE$ . Biết rằng bốn điểm $B,E,D,C$ cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
-
A.
Tâm là trọng tâm tam giác $ABC$ và bán kính $R = \dfrac{2}{3}AI$ với $I$ là trung điểm của $BC$.
-
B.
Tâm là trung điểm $AB$ và bán kính là $R = \dfrac{{AB}}{2}$
-
C.
Tâm là giao điểm của $BD$ và $EC$ , bán kính là $R = \dfrac{{BD}}{2}$
-
D.
Tâm là trung điểm $BC$ và bán kính là $R = \dfrac{{BC}}{2}$
Sử dụng: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
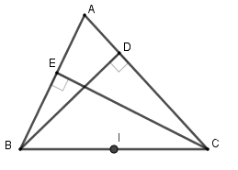
Gọi $I$ là trung điểm của $BC$.
Xét tam giác $BEC$ vuông tại $E$ có $EI = IB = IC = \dfrac{{BC}}{2}$ (vì $EI$ là đường trung tuyến ứng với cạnh huyền)
Xét tam giác $BDC$ vuông tại $D$ có $DI = IB = IC = \dfrac{{BC}}{2}$ (vì $DI$ là đường trung tuyến ứng với cạnh huyền)
Từ đó ta có $ID = IE = IB = IC = \dfrac{{BC}}{2}$ nên $I$ là tâm đường tròn ngoại tiếp tứ giác $DEBC$ và bán kính $R = \dfrac{{BC}}{2}$.
Đáp án : D








Danh sách bình luận