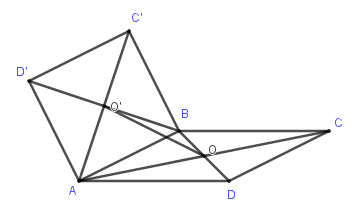
Trong không gian cho hai hình vuông $ABCD$ và $ABC'D'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm $O$ và $O'$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và $\overrightarrow {OO'} $?

Do \(O,O'\) là tâm các hình vuông \(ABCD,ABC'D'\) nên \(O,O'\) là trung điểm của \(BD,BD'\).

Do đó \(OO'\) là đường trung bình của tam giác \(BDD'\) \( \Rightarrow \overrightarrow {OO'}  = \dfrac{1}{2}\overrightarrow {DD'} \)

Ta có:

\(\overrightarrow {AB} .\overrightarrow {OO'}  = \overrightarrow {AB} .\dfrac{1}{2}\overrightarrow {DD'}  = \dfrac{1}{2}.\overrightarrow {AB} \left( {\overrightarrow {AD'}  - \overrightarrow {AD} } \right)\) \( = \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {AD'}  - \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {AD}  = 0 - 0 = 0\)

Do đó góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {OO'} \) bằng \({90^0}\)