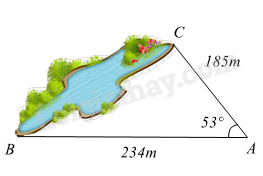
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
-
A.
\(190m\)
-
B.
\(191m\)
-
C.
\(192m\)
-
D.
\(193m\)
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow BD = AB - AD.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
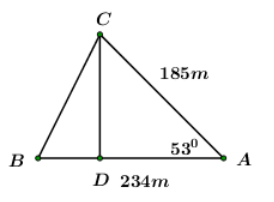
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\ \Rightarrow CD = 185.\sin {53^0}.\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow AD = 185.\cos {53^0}.\\ \Rightarrow BD = AB - AD = 234 - 185.\cos {53^0}.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
\(\begin{array}{l}B{C^2} = B{D^2} + C{D^2} = {\left( {234 - 185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {\left( {185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {185^2}\\ \Leftrightarrow B{C^2} \approx 36875,86\\ \Rightarrow BC \approx 192\,m.\end{array}\)
Đáp án : C

Các bài tập cùng chuyên đề
Một máy bay đang bay ở độ cao $10km$ so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là ${15^0}$ thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến hai chữ số phần thập phân)
-
A.
$37,32\,km$
-
B.
$373,2\,km$
-
C.
$38,32\,km$
-
D.
$37,52\,km$
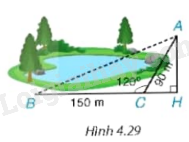
Một bạn muốn tính khoảng cách giữa hai điểm A và B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^0}\) (H.4.29) . Hãy tính AB giúp bạn.
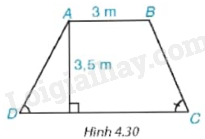
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là \(\tan D = 1,25.\) Độ dốc của sườn BC, tức là \(\tan C = 1,5.\) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.38), điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB.
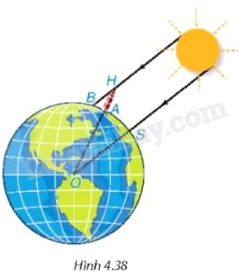
Một người quan sát tại ngọn hải đăng ở vị trí cao 149 m so với mặt nước biển thì thấy một du thuyền ở xa với góc nghiêng xuống là 27o (Hình 1). Hỏi thuyền cách xa chân hải đăng bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?
A. 292 m
B. 288 m
C. 312 m
D. 151 m
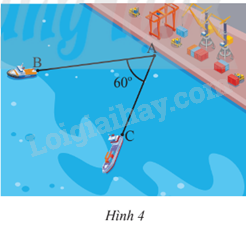
Hai điểm tàu thủy B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60o (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lý/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?
Hình 28 minh hoạ một máy bay cất cánh từ vị trí \(A\) trên đường băng của sân bay và bay theo đường thẳng \(AB\) tạo với phương nằm ngang \(AC\) một góc là \(20^\circ \). Sau 5 giây, máy bay ở độ cao \(BC = 110m\). Có thể tính khoảng cách \(AB\) bằng cách nào?

Hãy giải bài toán ở phần mở đầu và tính \(AB\) trong Hình 29b (làm tròn kết quả đến hàng phần trăm của mét).

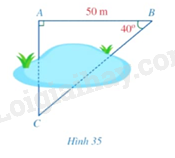
Hình 35 mô tả ba vị trí \(A,B,C\) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ \(C\) đến \(A\) và từ \(C\) đến \(B\). Biết \(AB = 50m\), \(\widehat {ABC} = 40^\circ \). Tính khoảng cách \(CA\) và \(CB\) (làm tròn kết quả đến hàng đơn vị của mét).
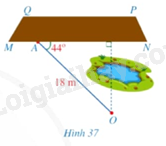
Trong công việc, người ta cần ước lượng khoảng cách từ vị trí \(O\) đến khu đất có dạng hình thang \(MNPQ\) nhưng không thể đo được trực tiếp, khoảng cách đó được tính bằng khoảng cách từ \(O\) đến đường thẳng \(MN\). Người ta chọn vị trí \(A\) ở đáy \(MN\) và đo được \(OA = 18m,\widehat {OAN} = 44^\circ \) (Hình 37). Tính khoảng cách từ vị trí \(O\) đến khu đất (làm tròn kết quả đến hàng phần mười của mét).
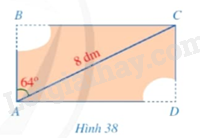
Một mảnh gỗ có dạng hình chữ nhật \(ABCD\) với đường chéo \(AC = 8dm\). Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh \(B\) và \(D\). Biết \(\widehat {BAD} = 64^\circ \) (Hình 38). Người ta cần biết độ dài \(AB\) và \(AD\) để khôi phục mảnh gỗ ban đầu. Độ dài \(AB,AD\) bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)?
Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) \(OA = 3m\) tạo với phương thẳng đứng một góc là \(\widehat {AOH} = 43^\circ \) thì khoảng cách \(AH\) từ em bé đến vị trí cân bằng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

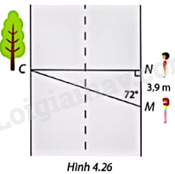
Trong Hình 4.26, bạn Mai và bạn Nam đứng ở vị trí điểm M và N ở cùng một bên lề đường và cây xanh C nằm đối diện vị trí Nam đứng ở phía bên kia đường. Tính chiều rộng NC của con đường.
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
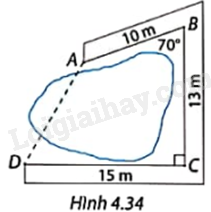
Người ta làm một con đường gồm ba đoạn AB, BC, CD bao quanh hồ nước như Hình 4.34. Tính khoảng cách AD.
Gợi ý: Từ điểm A, kẻ đường vuông góc AH xuống BC và AK xuống CD.
Một máy bay đang bay ở độ cao \(12km\) so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là \({12^0}\) thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến một chữ số phần thập phân)
-
A.
\(56,6\,km\)
-
B.
\(56,5\,km\)
-
C.
\(55,6\,km\)
-
D.
\(57\,km\)
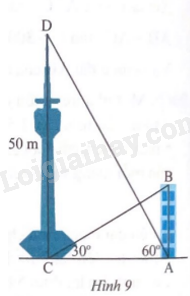
Từ chân một tháp cao 50 m người ta nhìn thấy đỉnh của một toà nhà với góc nâng 30o. Trong khi đó từ chân toà nhà, người ta lại nhìn thấy đỉnh tháp với góc nâng 60o. Tính chiều cao của toà nhà.
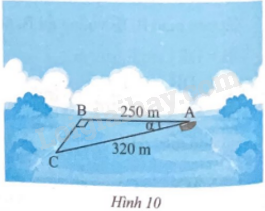
Tại khúc sông rộng 250 m, một chiếc thuyền đang đậu tại vị trí A và muốn di chuyển đến vị trí B bên kia bờ sông (Hình 10). Tuy nhiên, do chịu ảnh hưởng của dòng nước nên thuyền đã di chuyển đến vị trí C. Hãy xác định xem dòng nước đã làm chiếc thuyền đó di chuyển lệch đi một góc bao nhiêu dộ so với dự tính ban đầu.
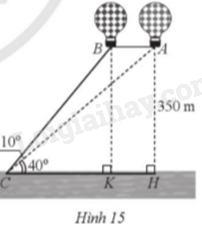
Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được \(\widehat {ACH} = 40^\circ ,\widehat {ACB} = 10^\circ \) (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).
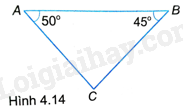
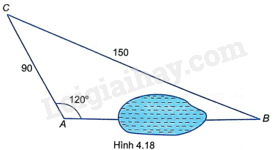
Hai trạm quan trắc tàu biển đặt ở hai mỏm núi A và B cách nhau 2km, nhìn thấy chiếc tàu C ở phía xa với \(\widehat {CAB} = {50^o},\widehat {CBA} = {45^o}\) (H.4.14). Hỏi tàu còn cách đường thẳng AB bao nhiêu mét?
Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800m. Khẩu pháo cao xa ngắm chiếc máy bay đó dưới một góc \({35^o}\) so với phương nằm ngang. Tìm khoảng cách từ pháo cao xạ đến máy bay (làm tròn đến mét).
Từ một đài quan sát ở cạnh bờ biển, có độ cao 300m so với mặt biển, nhìn thấy một con tàu dưới một góc \({25^o}\) (so với phương nằm ngang của mực nước biển (H.4.15)). Hỏi khoảng cách từ tàu đến đài quan sát xấp xỉ bao nhiêu mét?

Tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước (không đo trực tiếp được), biết khoảng cách từ một địa điểm C đến A và đến B là \(CA = 90m\), \(CB = 150m,\;\widehat {CAB} = {120^o}\) (làm tròn đến m) (H.4.18).
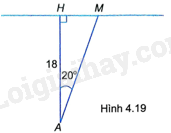
Một cầu thủ đứng cách khung thành 18m, đá quả bóng sát mặt đất, nghiêng một góc \({20^o}\) so với phương vuông góc với khung thành, tới điểm M của khung thành (H.4.19). Tính khoảng cách từ cầu thủ đến điểm M (làm tròn đến dm).
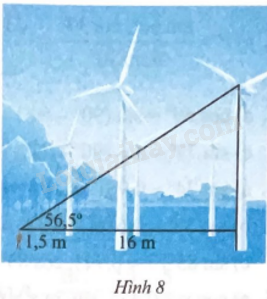
Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5o . Tính khoảng cách từ tâm của cánh quạt đến mặt đất, biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.
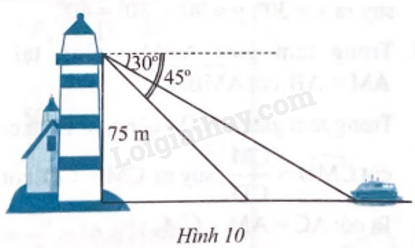
Một người đứng trên một tháp hải đăng ở vị trí cao 75 m so với mặt nước biển đã quan sát hai lần thấy một chiếc thuyền đang hướng về phía tháp hải đăng với góc hạ lần lượt là 30o và 45o (Hình 10). Hỏi thuyền đi được bao nhiêu mét giữa hai lần quan sát?
Một khối u (ở vị trí A) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia (ở vị trí B) cách hình chiếu của khối u (ở vị trí C) trên da mặt là 8,3 cm (Hình 19).
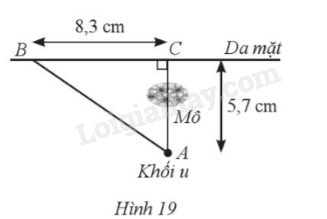
a) Hỏi góc tạo bởi chùm tia gamma với da mặt là bao nhiêu độ (làm tròn kết quả đến hàng phần mười)?
b) Chùm tia phải đi một đoạn dài bao nhiêu centimét để đến được khối u (làm tròn kết quả đến hàng phần mười).
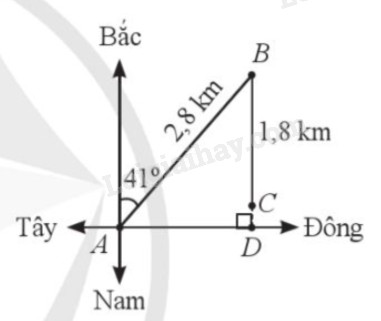
Một thuỷ thủ lái thuyền từ bờ (ở vị trí A) ra biển theo hướng Đông Bắc với góc nghiêng so với hướng Bắc là 41°. Đi được 2,8 km thì người đó phát hiện sắp hết nhiên liệu (ở vị trí B), vội quay thuyền vào bờ theo hướng Nam. Người đó đi tiếp được 1,8 km thì thuyền bị tắt máy (ở vị trí C) (Hình 31). Hỏi lúc đó thuyền còn cách bờ bao xa (làm tròn kết quả đến hàng phần mười của kilômét)?
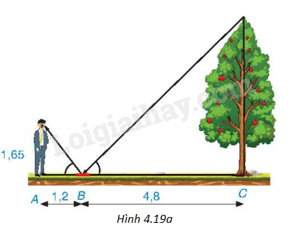
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65m. Tính chiều cao của cây (H.4.19a).
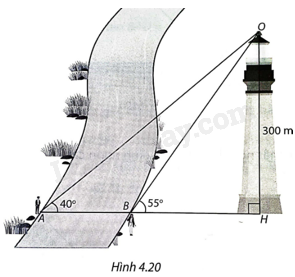
Để đo chiều rộng của một khúc sông, có hai người đã làm như sau: Hai người đứng ở hai vị trí A, B trên hai bên bờ sông, nhìn thấy đỉnh một tỏa tháp phía xa dưới góc \({40^o}\) và góc \({55^o}\) (H.4.20). Biết tòa tháp cao 300m, từ đó tính được khoảng cách AB. Em hãy cho biết, họ tính AB bằng bao nhiêu mét.
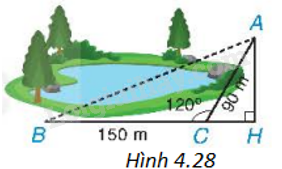
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^o}\) (H.4.28). Hãy tính AB giúp bạn.







Danh sách bình luận