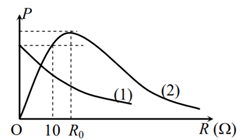
Cho đoạn mạch AB gồm biến trở R, cuộn dây không thuần cảm với độ tự cảm \(L = \dfrac{{0,6}}{\pi }H\), điện trở \(r > 10\Omega \), tụ điện có điện dung \(C = \dfrac{{{{10}^{ - 3}}}}{{3\pi }}F\) mắc nối tiếp. Đặt điện áp xoay chiều \(u = U\sqrt 2 cos100\pi t\left( V \right)\) (t tính bằng s) với \(U\) không đổi vào hai đầu A, B. Thay đổi giá trị biến trở R ta thu được đồ thị phụ thuộc của công suất tiêu thụ trên mạch vào giá trị R theo đường (1). Nối tắt cuộn dây và tiếp tục thì được đồ thị (2) biểu diễn sự phụ thuộc của công suất trên mạch vào giá trị R. Tỉ số \(\dfrac{{{R_0}}}{r}\) có giá trị là

 

Cảm kháng của cuộn dây là: \({Z_L} = \omega L = 100\pi .\dfrac{{0,6}}{\pi } = 60\,\,\left( \Omega  \right)\)

Dung kháng của tụ điện là: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 3}}}}{{3\pi }}}} = 30\,\,\left( \Omega  \right)\)

Khi chưa nối tắt cuộn dây: đồ thị (1)

Với \(R = 0 \Rightarrow {P_{1\max }} = \dfrac{{{U^2}\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\,\,\left( 1 \right)\)

Khi nối tắt cuộn dây: đồ thị (2)

Ta có công suất: \({P_2} = \dfrac{{{U^2}R}}{{{R^2} + {Z_C}^2}}\)

Nhận xét: với \(R = 10\Omega  \Rightarrow {P_2} = {P_{1\max }}\)

\(\begin{array}{l} \Rightarrow \dfrac{{{U^2}R}}{{{R^2} + {Z_C}^2}} = \dfrac{{{U^2}r}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} \Rightarrow \dfrac{{10}}{{{{10}^2} + {{30}^2}}} = \dfrac{r}{{{r^2} + {{\left( {60 - 30} \right)}^2}}}\\ \Rightarrow 10{r^2} + 9000 = 1000r \Rightarrow 10{r^2} - 1000r + 9000 = 0\\ \Rightarrow \left[ \begin{array}{l}r = 10\,\,\left( \Omega  \right)\,\,\left( {loai} \right)\\r = 90\,\,\left( \Omega  \right)\,\,\left( {t/m} \right)\end{array} \right.\end{array}\)

Với \(R = {R_0} \Rightarrow {P_{2\max }} \Leftrightarrow {R_0} = {Z_C} = 30\,\,\left( \Omega  \right)\)

Vậy \(\dfrac{{{R_0}}}{r} = \dfrac{{30}}{{90}} = \dfrac{1}{3}\)