Đề bài
Cho 4 điểm không đồng phẳng $A,\,\,B,\,\,C,\,\,D.$ Gọi $I,\,\,K$ lần lượt là trung điểm của $AD$ và $BC.$ Giao tuyến của $\left( {IBC} \right)$ và $\left( {KAD} \right)$ là:
-
A.
\(IK.\)
-
B.
\(BC.\)
-
C.
\(AK.\)
-
D.
\(DK.\)
Phương pháp giải
- Chứng minh \(I,K\) thuộc cả hai mặt phẳng, từ đó suy ra \(IK\) là giao tuyến.
Lời giải của GV Loigiaihay.com
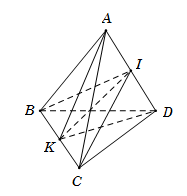
Điểm $K$ là trung điểm của $BC$ suy ra $K \in \left( {IBC} \right)\,\, \Rightarrow \,\,IK \subset \left( {IBC} \right).$
Điểm $I$ là trung điểm của $AD$ suy ra $I \in \left( {KAD} \right)\,\, \Rightarrow \,\,IK \subset \left( {KAD} \right).$
Vậy giao tuyến của hai mặt phẳng $\left( {IBC} \right)$ và $\left( {KAD} \right)$ là $IK.$
Đáp án : A
