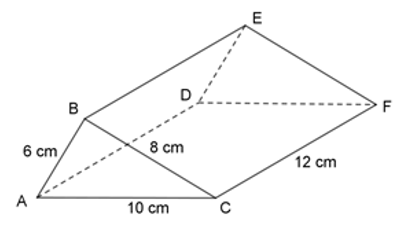
Cho hình lăng trụ đứng \(ABC.DEF\), đáy là tam giác \(ABC\) có \(AB = 6\,cm,BC = 8\,cm,AC = 10\,cm\) và chiều cao của lăng trụ là \(12\,cm\).

Ta có:

\(\begin{array}{l}A{B^2} + B{C^2} = {6^2} + {8^2} = 100\\A{C^2} = {10^2} = 100\\ \Rightarrow A{B^2} + B{C^2} = A{C^2}\end{array}\)

Áp dụng định lý đảo của định lý Pitago ta có tam giác \(ABC\) là tam giác vuông tại \(B\).

Diện tích xung quanh của hình lăng trụ \(ABC.DEF\) là:

            \({S_{xq}} = (6 + 8 + 10).12 = 288\;c{m^2}\)

Diện tích đáy \(ABC\) của hình lăng trụ \(ABC.DEF\) là:

            \({S_d} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.6.8 = 24\;c{m^2}\)

Diện tích toàn phần của hình lăng trụ \(ABC.DEF\) là:

            \({S_{tp}} = {S_{xq}} + 2.{S_d} = 288 + 2.24 = 336c{m^2}\).

Thể tích hình lăng trụ đứng \(ABC.DEF\) là: \(V = {S_d}.h = 24.12 = 288c{m^3}_{}\).