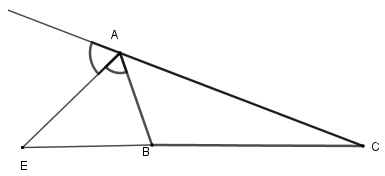
Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc \(A\). Hãy chọn câu sai:
-
A.
\(\dfrac{{CE}}{{AC}} = \dfrac{{BE}}{{AB}}\)
-
B.
\(\dfrac{{AB}}{{CE}} = \dfrac{{AC}}{{BE}}\)
-
C.
\(\dfrac{{AB}}{{BE}} = \dfrac{{AC}}{{CE}}\)
-
D.
\(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\)
Sử dụng tính chất tia phân giác góc ngoài của tam giác:
Định lý: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Chú ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
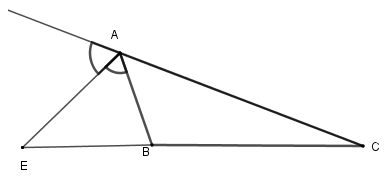
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên \(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\) hay D đúng.
\(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\)\( \Rightarrow \dfrac{{AB}}{{BE}} = \dfrac{{AC}}{{CE}}\) nên C đúng.
\(\dfrac{{AB}}{{BE}} = \dfrac{{AC}}{{CE}}\)\( \Rightarrow \dfrac{{CE}}{{AC}} = \dfrac{{BE}}{{AB}}\) nên A đúng.
Chỉ có B sai.
Đáp án : B
