Đề bài
Cho tứ giác \(ABCD\) có \(O\) là giao điểm hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\). Đường thẳng qua \(B\) và song song với \(AD\) cắt \(AC\) ở \(G\). Chọn kết luận sai?
-
A.
\(\dfrac{{OE}}{{OB}} = \dfrac{{OA}}{{OC}}\)
-
B.
\(\dfrac{{EG}}{{AB}} = \dfrac{{OE}}{{OB}}\)
-
C.
\(\dfrac{{OB}}{{OD}} = \dfrac{{OG}}{{OA}}\)
-
D.
\(EG//CD\)
Lời giải của GV Loigiaihay.com
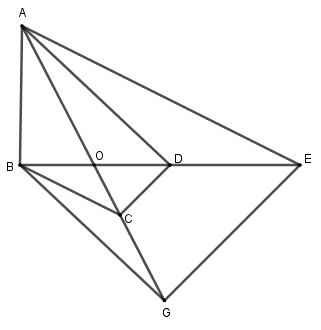
Theo định lí Ta-let:
Ta có: \(AE//BC\) nên \(\dfrac{{OE}}{{OB}} = \dfrac{{OA}}{{OC}}\) (1) hay A đúng.
\(BG//AD\) nên \(\dfrac{{OB}}{{OD}} = \dfrac{{OG}}{{OA}}\) (2) hay C đúng.
Từ (1) và (2) suy ra: \(\dfrac{{OE}}{{OB}}.\dfrac{{OB}}{{OD}} = \dfrac{{OA}}{{OC}}.\dfrac{{OG}}{{OA}}\) hay \(\dfrac{{OE}}{{OD}} = \dfrac{{OG}}{{OC}}\), do đó \(EG//CD\) (định lí Ta-let đảo) hay D đúng.
Vậy B sai.
Đáp án : B
