Chiếu một tia sáng SI đến vuông góc với màn E tại I. Trên đường đi của tia sáng, người ta đặt tại đỉnh A của một lăng kính thủy tinh có góc chiết quang \(A = {5^0}\) , chiết suất \(n = 1,5\) sao cho SI vuông góc với mặt phân giác của góc chiết quang A, tia sáng ló đến màn E tại điểm J. Đoạn IJ =?Biết rằng màn E đặt cách đỉnh A của lăng kính một khoảng 1m.
-
A.
8,72cm
-
B.
2,5m
-
C.
2,5cm
-
D.
4,36cm
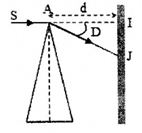
Vì góc chiết quang nhỏ nên ta dễ suy ra công thức tính góc lệch giữa tia tới và tia ló là:
\(D = (n - 1)A\)
Từ hình vẽ, ta có:
\(\tan D = \frac{{{\rm{IJ}}}}{{AI}}\)
Vì A nhỏ, nên D nhỏ
Ta có: \(\tan D \approx D\)
$ \leftrightarrow (n - 1)A = \frac{{IJ}}{{AI}} = \frac{{{\text{IJ}}}}{d} \to I{\text{J}} = d(n - 1)A = 1.(1,5 - 1).\frac{{5.\pi }}{{180}} = 0,0436m = 4,36cm$
Đáp án : D
Góc chiết quang tính bằng rad\({1^0} = \frac{\pi }{{180}}{\rm{r}}a{\rm{d}}\)
