Một con lắc đơn chiều dài \(l = 1,2m\), một đầu gắn với vật khối lượng \(100g\). Thẳng phía dưới điểm treo cách điểm treo một đoạn \(\dfrac{l}{2}\) có một cái đinh. Kéo vật ra khỏi vị trí cân bằng sao cho dây treo hợp với phương thẳng đứng một góc \({30^0}\) rồi thả nhẹ. Bỏ qua mọi sức cản và ma sát, lấy \(g = 10m/{s^2}\)

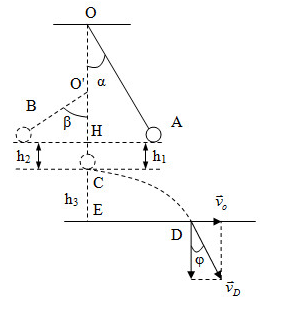
Chọn gốc thế năng tại vị trí cân bằng (C)

+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\)  (1)

Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)

Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)

 Từ hình ta có:

\(\begin{array}{l}cos\beta  = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta  = 42,{9^0}\end{array}\)

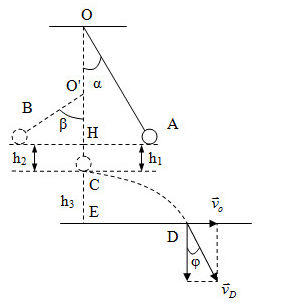
Chọn gốc thế năng tại vị trí cân bằng (C)

+ Áp dụng định luật bảo toàn cơ năng tại hai điểm A và B, ta có:

\({{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg{h_1} = mg{h_2} \to {h_1} = {h_2}\)  (1)

Mặt khác, ta có: \({h_1} = l\left( {1 - cos\alpha } \right)\)

Thế vào (1) ta suy ra: \({h_1} = {h_2} = l\left( {1 - cos\alpha } \right) = 1,2\left( {1 - cos{{30}^0}} \right) = 0,1607m\)

Từ hình ta có:

\(\begin{array}{l}cos\beta  = \dfrac{{O'H}}{{O'B}} = \dfrac{{\dfrac{l}{2} - {h_1}}}{{\dfrac{l}{2}}} = \dfrac{{\dfrac{{1,2}}{2} - 0,1607}}{{\dfrac{{1,2}}{2}}} = 0,732\\ \to \beta  = 42,{9^0}\end{array}\)

+ Ta có cơ năng tại B: \({{\rm{W}}_B} = mg{h_2}\)

Cơ năng tại C: \({{\rm{W}}_C} = \dfrac{1}{2}mv_C^2\)

+ Áp dụng định luật bảo toàn cơ năng tại 2 vị trí B và C, ta có:

\({{\rm{W}}_B} = {{\rm{W}}_C} \leftrightarrow mg{h_2} = \dfrac{1}{2}mv_C^2 \to {v_C} = \sqrt {2g{h_2}}  = \sqrt {2.10.0,1607}  = 1,79m/s\)

+ Khi quay lại C, dây bị đứt chuyển động của vật coi như chuyển động ném ngang với vận tốc ban đầu \({v_0} = 1,79m/s\)

Áp dụng định luật bảo toàn cơ năng cho điểm C và D (chọn gốc thế năng tại mặt đất)

\({{\rm{W}}_C} = {{\rm{W}}_D} \leftrightarrow \dfrac{1}{2}mv_C^2 + mg{h_3} = \dfrac{1}{2}mv_D^2\)  (2)

Ta có: \(\left\{ \begin{array}{l}m = 100g = 0,1kg\\{v_C} = 1,79m/s\\{h_3} = 2 - l = 2 - 1,2 = 0,8m\end{array} \right.\)

Thế vào (2), ta được:

\(\begin{array}{l}\dfrac{1}{2}.0,1.1,{79^2} + 0,1.10.0,8 = \dfrac{1}{2}0,1.v_D^2\\ \to {v_D} = 4,38m/s\end{array}\)