Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm $M$ nằm trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm $M$ nhất, sau đó một khoảng thời gian ngắn nhất là $\Delta t$ thì vật gần điểm $M$ nhất. Độ lớn vận tốc của vật sẽ đạt được cực đại vào thời điểm:
-
A.
$t + \dfrac{{\Delta t}}{2}$
-
B.
$t + \Delta t$
-
C.
$\dfrac{{t + \Delta t}}{2}$
-
D.
$\dfrac{t}{2} + \dfrac{{\Delta t}}{4}$
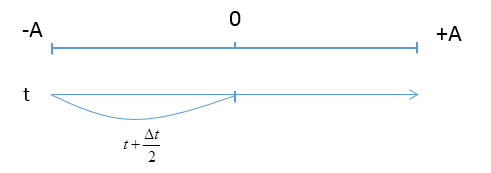
Sử dụng trục thời gian suy ra từ vòng tròn
Giả sử điểm M nằm phía ngoài gần biên dương
Ta có, tại thời điểm t vật đang ở biên âm
Tại t + ∆t: vật đang ở biên dương
=> ∆t là khoảng thời gian vật đi từ biên âm đến biên dương
\( \to \Delta t = \frac{T}{2}\)
Độ lớn vận tốc của vật đạt cực đại khi vật ở vị trí cân bằng
=> Độ lớn vận tốc của vật sẽ đạt được cực đại vào thời điểm: \(t + \frac{{\Delta t}}{2}\)
Đáp án : A








Danh sách bình luận