Đề bài
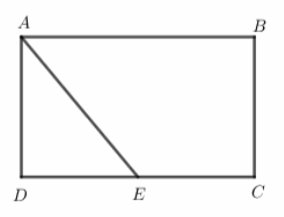
Hình chữ nhật \(ABCD\) có diện tích \(3600c{m^2}\). \(E\) là trung điểm của \(DC.\) Tính diện tích tam giác \(ADE.\)
-
A.
\(900\,c{m^2}\)
-
B.
\(800\,c{m^2}\)
-
C.
\(600\,c{m^2}\)
-
D.
\(190\,cm^2\)
Phương pháp giải
Quan sát hình vẽ, ta thấy diện tích tam giác \(ADE\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật.
Từ đó, muốn tính diện tích tam giác \(ADE\) ta lấy diện tích hình chữ nhật chia cho 4.
Lời giải của GV Loigiaihay.com
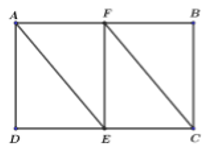
Lấy F là trung điểm của AB, nối \(EF\), \(FC\).
Hình chữ nhật ABCD được phân thành 4 hình tam giác có diện tích bằng nhau và bằng diện tích tam giác \(ADE\).
Vậy diện tích tam giác \(ADE\) là: \(3600:4 = 900\,\left( {c{m^2}} \right)\).
Đáp số: \(900\,c{m^2}\).
Đáp án : A
