Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).
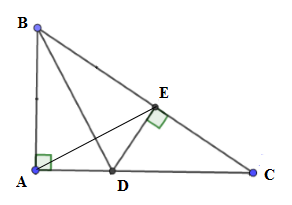
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).

Chọn câu đúng.
Chọn câu đúng.
Tam giác \(ABE\) là tam giác cân tại \(B\)
Tam giác \(ABE\) là tam giác cân tại \(A\)
Tam giác \(ABE\) là tam giác cân tại \(E\)
Tam giác \(ADE\) là tam giác cân tại \(A\)
Đáp án: A
Sử dụng cặp tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn.
Xét hai tam giác vuông ABD và EBD có:
BD chung; \(\widehat {ABD} = \widehat {EBD}\) (gt)
\( \Rightarrow \Delta ABD = \Delta EBD \,(ch - gn)\)
\( \Rightarrow BA = BE;DA = DE\) (hai cạnh tương ứng)
Suy ra: \(\Delta ABE\) cân tại \(B\) và \(\Delta ADE\) cân tại D.

So sánh độ dài các đoạn thẳng \(AD\) và \(DC\).
So sánh độ dài các đoạn thẳng \(AD\) và \(DC\).
\(DC > AD\)
\(DC < AD\)
\(DC = AD\)
Không đủ điều kiện so sánh
Đáp án: A
Trong tam giác vuông, cạnh huyền là cạnh có độ dài lớn nhất.
Do tam giác \(DEC\) vuông tại \(E\) nên \(DC > DE;\) mà \(DE = AD\) (theo câu trước)
Suy ra \(DC > AD.\)
Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
\(12\,cm\)
\(13\,cm\)
\(16\,cm\)
\(15\,cm\)
Đáp án: B
Sử dụng định lý Pytago: “Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”.
Áp dụng định lý Py-ta-go vào tam giác vuông BDE có:
\(B{D^2} = B{E^2} + D{E^2} \)
\(B{D^2} = BE{}^2 + A{D^2}\) (do \(AD = DE\) (theo câu trước))
suy ra \( BD = \sqrt {B{E^2} + A{D^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13(cm)\).








Danh sách bình luận