Đề bài

Đặt điện áp xoay chiều u = U₀cos(ωt + φ) (V) (U₀ và ω không đổi) vào hai đầu đoạn mạch gồm điện trở $R$, tụ điện và cuộn cảm thuần mắc nối tiếp. Biết biểu thức cường độ dòng điện trong mạch là ${i_1} = \sqrt 5 {\rm{cos(}}\omega {\rm{t + }}\dfrac{\pi }{3})(A)$ . Nếu ngắt bỏ tụ điện $C$ thì cường độ dòng điện trong mạch là ${i_2} = \sqrt 5 {\rm{cos(}}\omega {\rm{t - }}\dfrac{\pi }{6})(A)$. Nếu ngắt bỏ cuộn cảm thì cường độ dòng điện trong mạch là

A.

${i_3} = \sqrt 2 {\rm{cos(}}\omega {\rm{t - 1,107}})(A)$
B.

${i_3} = \sqrt 2 {\rm{cos(}}\omega {\rm{t + 1,37}})(A)$
C.

${i_3} = \dfrac{5}{{\sqrt 2 }}{\rm{cos(}}\omega {\rm{t - 1,107}})(A)$
D.

${i_3} = \dfrac{5}{{\sqrt 2 }}{\rm{cos(}}\omega {\rm{t + 1,37}})(A)$

Phương pháp giải

Đoạn mạch RLC nối tiếp có u_R cùng pha i, u_L sớm pha π/2 so với i và u_C chậm pha π/2 so với i

Tổng trở mạch RLC là $Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} $

Định luật Ôm cho đoạn mạch : I = U/Z

Lời giải của GV Loigiaihay.com

Sử dụng giản đồ vec tơ ghép:

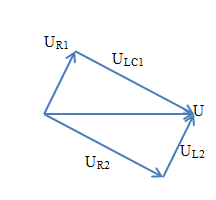
Vì I bằng nhau nên U_R1 = U_R2 vậy hình tạo thành là hình vuông

Ta có:

$\left\{ \begin{array}{l}{Z_1} = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \\{Z_2} = \sqrt {{R^2} + {Z_L}^2} \end{array} \right.$

Vì đạt cùng điện áp hiệu dụng, mà giả thiết hai dòng điện có cùng giá trị hiệu dụng nên ta có:

${Z_1} = {Z_2} \Leftrightarrow \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{R^2} + Z_L^2} $

$ \Leftrightarrow {({Z_L} - {Z_C})^2} = Z_L^2 \Leftrightarrow \left| {{Z_L} - {Z_C}} \right| = {Z_L}$

$ \Leftrightarrow {Z_C} = 2{{\rm{Z}}_L}$

Theo bài ra, phương trình điện áp hai đầu đoạn mạch là:

$u = {U_0}\cos \left( {\omega t + \varphi } \right)\left( V \right)$

Độ lệch pha của dòng điện và điện áp trong mạch trong hai lần, lần lượt là:

$\left\{ \begin{array}{l}\frac{{{Z_C} - {Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi - \left( { - \frac{\pi }{6}} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{{{Z_L}}}{R} = \frac{\pi }{3} - \varphi \\\frac{{{Z_L}}}{R} = \varphi + \frac{\pi }{6}\end{array} \right.$

$ \Rightarrow \frac{\pi }{3} - \varphi = \varphi + \frac{\pi }{6} \Leftrightarrow \varphi = \frac{\pi }{{12}}$

Mà U_R1 = U_L2 => $R = {Z_L} = \left| {{Z_L} - {Z_C}} \right| \Rightarrow R = {Z_L} = \dfrac{1}{2}{Z_C}$

Chuẩn hóa R = 1. Ta có :

${I_{01}} = \dfrac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\sqrt {{1^2} + {{(2 - 1)}^2}} }} \Rightarrow I = \dfrac{U}{\sqrt 2} V$

${I_{03}} = \dfrac{U}{{{Z_C}}} = \dfrac{U}{2} = \sqrt 2 A$

Mà i₃ chỉ có tụ và điện trở nên pha ban đầu của i₃ = 1,37 rad

Đáp án : B

Báo lỗi/Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Đặt điện áp $u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)$ vào hai đầu điện trở thuần thì cường độ dòng điện qua R là: